基于动量轮动策略的有效性分析
引言
动量效应是金融市场中一种重要的现象,指过去表现较好的资产在未来短期内往往继续表现 较好,而过去表现较差的资产则继续表现较差。基于动量效应的交易策略已经被广泛研究和 应用。
在股票市场中,大盘股和小盘股通常具有不同的风险收益特征和市场表现。本研究旨在探索 一种基于动量的轮动策略,通过比较大盘股和小盘股的相对强度,动态调整投资组合的配置, 以获取超额收益。
我们将使用R语言实现这一策略,并通过历史数据验证其有效性。同时,我们会优化策略参数, 测试参数敏感性,并在样本外数据上验证策略的稳健性。
数据准备与分析
首先加载必要的R包并获取股票数据。我们将选取多只大盘股和小盘股作为研究对象。
# 加载必要的R包
library(quantmod)
library(PerformanceAnalytics)
library(foreach)
library(doParallel)
library(ggplot2)
library(dplyr)
library(tidyr)
library(caret)
library(magrittr)
接下来,我们获取股票数据。我们将选择10只大盘股和10只小盘股作为样本。大盘股选取标 普500指数成分股中市值最大的10只,小盘股选取罗素2000指数成分股中市值最小的10只。
# 设置起止日期
start_date <- "2018-01-01"
end_date <- "2023-01-01"
out_of_sample_date <- "2023-01-02"
end_oos_date <- "2023-12-31"
# 大盘股列表
large_cap_symbols <- c("AAPL", "MSFT", "AMZN", "TSLA")
# 小盘股列表
small_cap_symbols <- c("ARQT", "AVXL", "BPMC", "CELZ")
# 所有股票代码
all_symbols <- c(large_cap_symbols, small_cap_symbols)
# 获取股票数据
stock_data <- list()
for (symbol in all_symbols) {
tryCatch(
{
stock_data_raw <- getSymbols(symbol,
from = start_date,
to = end_date,
auto.assign = FALSE)
colnames(stock_data_raw) <- c("Open",
"High",
"Low",
"Close",
"Volume",
"Adjusted")
stock_data[[symbol]] <- stock_data_raw
cat("Successfully downloaded", symbol, "\n")
},
error = function(e) {
cat("Error downloading", symbol, ":", conditionMessage(e), "\n")
}
)
}
## Successfully downloaded AAPL
## Successfully downloaded MSFT
## Successfully downloaded AMZN
## Successfully downloaded TSLA
## Successfully downloaded ARQT
## Successfully downloaded AVXL
## Successfully downloaded BPMC
## Successfully downloaded CELZ
# 过滤掉下载失败的股票
valid_symbols <- names(stock_data)
large_cap_symbols <- large_cap_symbols[large_cap_symbols %in% valid_symbols]
small_cap_symbols <- small_cap_symbols[small_cap_symbols %in% valid_symbols]
# 获取样本外数据
oos_data <- list()
for (symbol in valid_symbols) {
tryCatch(
{
oss_data_raw <- getSymbols(symbol,
from = out_of_sample_date,
to = end_oos_date,
auto.assign = FALSE)
colnames(oss_data_raw) <- c("Open",
"High",
"Low",
"Close",
"Volume",
"Adjusted")
oos_data[[symbol]] <- oss_data_raw
cat("Successfully downloaded OOS data for", symbol, "\n")
},
error = function(e) {
cat("Error downloading OOS data for", symbol, ":", conditionMessage(e), "\n")
}
)
}
## Successfully downloaded OOS data for AAPL
## Successfully downloaded OOS data for MSFT
## Successfully downloaded OOS data for AMZN
## Successfully downloaded OOS data for TSLA
## Successfully downloaded OOS data for ARQT
## Successfully downloaded OOS data for AVXL
## Successfully downloaded OOS data for BPMC
## Successfully downloaded OOS data for CELZ
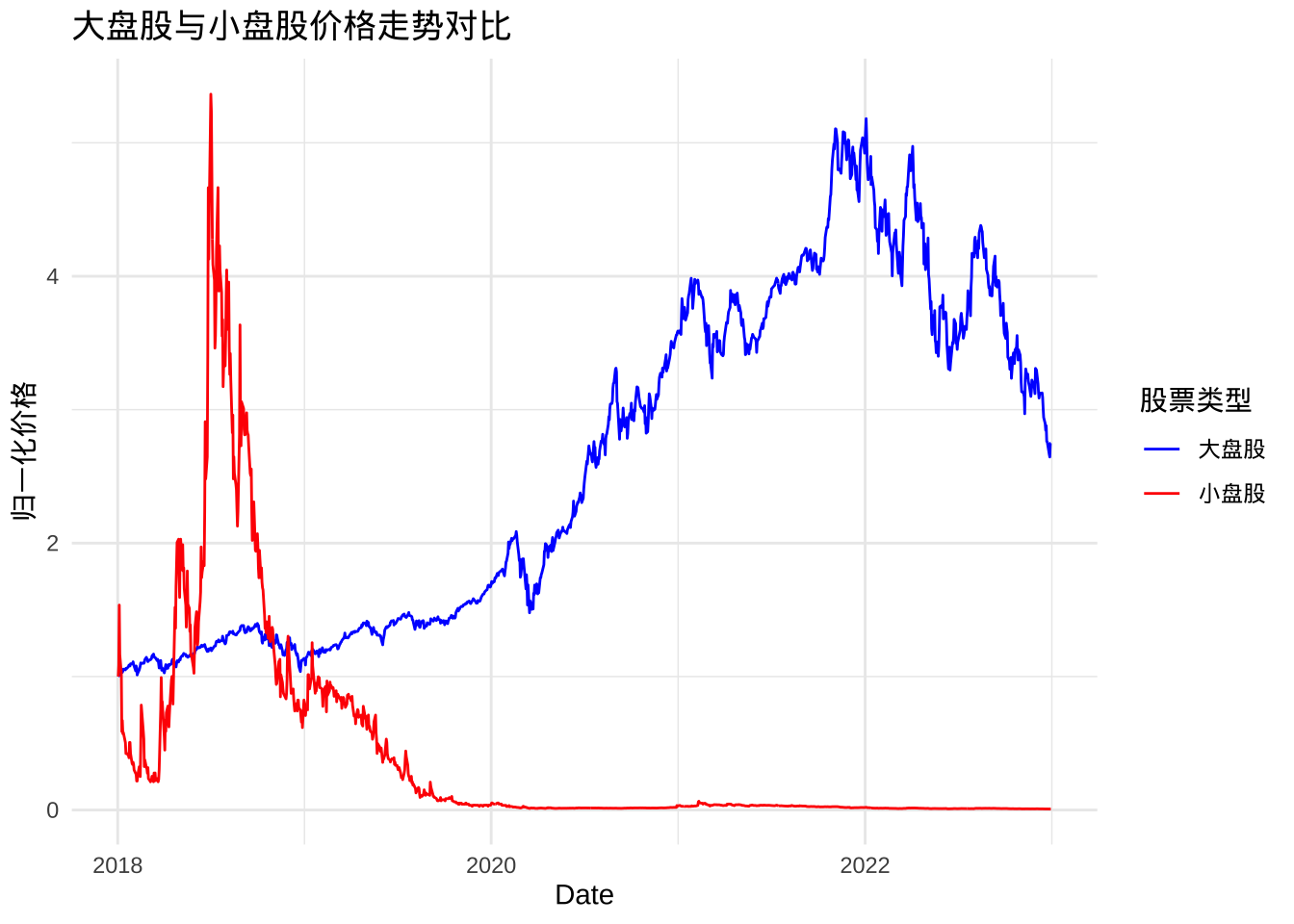
让我们计算并可视化大盘股和小盘股的平均价格走势,以便对数据有一个直观的了解。
# 函数:合并多只股票的收盘价并处理缺失值
merge_stock_prices <- function(symbols, stock_data_list) {
merged_prices <- NULL
for (symbol in symbols) {
# 提取单只股票的收盘价
stock_close <- Cl(stock_data_list[[symbol]])
# 如果是第一只股票,直接赋值
if (is.null(merged_prices)) {
merged_prices <- stock_close
colnames(merged_prices) <- symbol
} else {
# 合并多只股票,自动对齐日期
merged_prices <- merge(merged_prices, stock_close)
colnames(merged_prices)[ncol(merged_prices)] <- symbol
}
}
# 处理缺失值:使用前向填充和后向填充结合
merged_prices <- na.locf(merged_prices) # 前向填充
merged_prices <- na.locf(merged_prices, fromLast = TRUE) # 后向填充
return(merged_prices)
}
# 合并大盘股和小盘股的价格数据
large_cap_merged <- merge_stock_prices(large_cap_symbols, stock_data)
small_cap_merged <- merge_stock_prices(small_cap_symbols, stock_data)
# 确保两个数据集具有相同的日期范围
common_dates <- intersect(index(large_cap_merged), index(small_cap_merged))
large_cap_merged <- large_cap_merged[common_dates]
small_cap_merged <- small_cap_merged[common_dates]
# 计算平均价格
large_cap_avg <- rowMeans(large_cap_merged)
small_cap_avg <- rowMeans(small_cap_merged)
# 归一化价格
large_cap_norm <- large_cap_avg / large_cap_avg[1]
small_cap_norm <- small_cap_avg / small_cap_avg[1]
# 创建绘图数据框
price_data <- data.frame(
Date = as.Date(index(large_cap_merged)),
Large_Cap = as.numeric(large_cap_norm),
Small_Cap = as.numeric(small_cap_norm)
)
# 使用ggplot2绘制对比图
library(ggplot2)
ggplot(price_data, aes(x = Date)) +
geom_line(aes(y = Large_Cap, color = "大盘股")) +
geom_line(aes(y = Small_Cap, color = "小盘股")) +
labs(
title = "大盘股与小盘股价格走势对比",
y = "归一化价格",
color = "股票类型"
) +
theme_minimal() +
scale_color_manual(values = c("大盘股" = "blue", "小盘股" = "red"))
动量轮动策略实现
下面我们实现基于动量的大盘股/小盘股轮动策略。该策略的核心思想是:比较大盘股和小盘 股的相对动量,选择动量更强的一组进行投资。
首先定义一个函数来实现这个策略:
# 改进的动量轮动策略函数
momentum_rotation_strategy <- function(large_cap_data, small_cap_data,
lookback_period = 20,
holding_period = 10,
rebalance_threshold = 0.05,
commission = 0.001) {
# 函数:计算单只股票的对数收益率
calculate_returns <- function(stock_data) {
colnames(stock_data) <- c("Open", "High", "Low", "Close", "Volume", "Adjusted")
close_prices <- Cl(stock_data)
returns <- dailyReturn(close_prices, type = "log")
colnames(returns) <- ""
return(returns)
}
# 计算所有股票的收益率
large_cap_returns_list <- lapply(large_cap_data, calculate_returns)
small_cap_returns_list <- lapply(small_cap_data, calculate_returns)
# 合并所有收益率数据,自动对齐日期
large_cap_returns_merged <- do.call(merge, large_cap_returns_list)
small_cap_returns_merged <- do.call(merge, small_cap_returns_list)
# 将所有NA值填充为0
large_cap_returns_merged <- na.fill(large_cap_returns_merged, fill = 0)
small_cap_returns_merged <- na.fill(small_cap_returns_merged, fill = 0)
# 确保两个数据集具有相同的日期范围
common_dates <- intersect(index(large_cap_returns_merged),
index(small_cap_returns_merged))
large_cap_returns_merged <- large_cap_returns_merged[common_dates]
small_cap_returns_merged <- small_cap_returns_merged[common_dates]
# 计算平均收益率(保持xts格式)
large_cap_avg_returns <- xts(rowMeans(large_cap_returns_merged),
order.by = index(large_cap_returns_merged)
)
small_cap_avg_returns <- xts(rowMeans(small_cap_returns_merged),
order.by = index(small_cap_returns_merged)
)
# 计算动量指标(lookback_period天的累计收益率)
large_cap_momentum <- xts(rep(0, length(large_cap_avg_returns)),
order.by = index(large_cap_avg_returns)
)
small_cap_momentum <- xts(rep(0, length(small_cap_avg_returns)),
order.by = index(small_cap_avg_returns)
)
for (i in (lookback_period + 1):length(large_cap_avg_returns)) {
large_cap_momentum[i] <- sum(large_cap_avg_returns[(i - lookback_period):i])
small_cap_momentum[i] <- sum(small_cap_avg_returns[(i - lookback_period):i])
}
# 初始化仓位(保持xts格式)
position <- xts(rep(0, length(large_cap_avg_returns)),
order.by = index(large_cap_avg_returns)
)
position[lookback_period + 1] <- ifelse(large_cap_momentum[lookback_period + 1] > small_cap_momentum[lookback_period + 1], 1, -1)
# 生成交易信号
for (i in (lookback_period + 2):length(large_cap_avg_returns)) {
# 每隔holding_period天重新评估一次
if ((i - lookback_period) %% holding_period == 0) {
# 计算动量差异
momentum_diff <- large_cap_momentum[i] - small_cap_momentum[i]
# 如果动量差异超过阈值,则切换仓位
if (abs(momentum_diff) > rebalance_threshold) {
position[i] <- ifelse(momentum_diff > 0, 1, -1)
} else {
# 否则保持原仓位
position[i] <- position[i - 1]
}
} else {
# 保持原仓位
position[i] <- position[i - 1]
}
}
# 计算策略收益(保持xts格式)
strategy_returns <- position * (large_cap_avg_returns - small_cap_avg_returns)
strategy_return <- na.fill(strategy_returns, fill = 0) # 将NA值填充为0
# 考虑交易成本
# 创建与position相同长度和索引的trades对象
trades <- xts(rep(0, length(position)), order.by = index(position))
trades <- abs(diff(position)) > 0
trades <- na.fill(trades, fill = "FALSE") # 将NA值填充为FALSE
commission_cost <- trades * commission
# 计算净收益(保持xts格式)
net_returns <- strategy_returns - commission_cost
net_returns <- na.fill(net_returns, fill = 0) # 将NA值填充为0
# 计算累积收益(保持xts格式)
cumulative_returns <- exp(cumsum(net_returns)) - 1
# 返回结果(同时包含xts和data.frame格式)
results_xts <- list(
Large_Cap_Returns = large_cap_avg_returns,
Small_Cap_Returns = small_cap_avg_returns,
Strategy_Returns = strategy_returns,
Commission_Cost = commission_cost,
Net_Returns = net_returns,
Cumulative_Returns = cumulative_returns,
Position = position,
Large_Cap_Momentum = large_cap_momentum,
Small_Cap_Momentum = small_cap_momentum
)
results_df <- data.frame(
Date = as.Date(index(large_cap_avg_returns)),
Large_Cap_Momentum = as.numeric(large_cap_momentum),
Small_Cap_Momentum = as.numeric(small_cap_momentum),
Position = as.numeric(position),
Large_Cap_Returns = as.numeric(large_cap_avg_returns),
Small_Cap_Returns = as.numeric(small_cap_avg_returns),
Strategy_Returns = as.numeric(strategy_returns),
Commission_Cost = as.numeric(commission_cost),
Net_Returns = as.numeric(net_returns),
Cumulative_Returns = as.numeric(cumulative_returns)
)
colnames(results_df) <- c(
"Date", "Large_Cap_Momentum", "Small_Cap_Momentum",
"Position", "Large_Cap_Returns", "Small_Cap_Returns",
"Strategy_Returns", "Commission_Cost",
"Net_Returns", "Cumulative_Returns"
)
return(list(df = results_df, xts = results_xts))
}
现在我们将这个策略应用到数据上,并评估其表现:
# 应用策略到数据
strategy_results <- momentum_rotation_strategy(
lapply(large_cap_symbols, function(symbol) stock_data[[symbol]]),
lapply(small_cap_symbols, function(symbol) stock_data[[symbol]])
)
# 计算买入持有策略的收益(保持xts格式)
buy_hold_large_cap <- exp(cumsum(strategy_results$xts$Large_Cap_Returns)) - 1
buy_hold_small_cap <- exp(cumsum(strategy_results$xts$Small_Cap_Returns)) - 1
buy_hold_equal <- (buy_hold_large_cap + buy_hold_small_cap) / 2
# 使用ggplot2绘制累积收益对比图
performance_data <- data.frame(
Date = as.Date(index(buy_hold_large_cap)),
Large_Cap = as.numeric(buy_hold_large_cap),
Small_Cap = as.numeric(buy_hold_small_cap),
Equal_Weight = as.numeric(buy_hold_equal),
Momentum = as.numeric(strategy_results$xts$Cumulative_Returns)
)
# 转换为长格式数据以便绘图
library(tidyr)
performance_data_long <- performance_data %>%
pivot_longer(cols = -Date,
names_to = "Strategy",
values_to = "Cumulative_Return")
# 绘制对比图
library(ggplot2)
ggplot(performance_data_long,
aes(x = Date,
y = Cumulative_Return,
color = Strategy)) +
geom_line() +
labs(
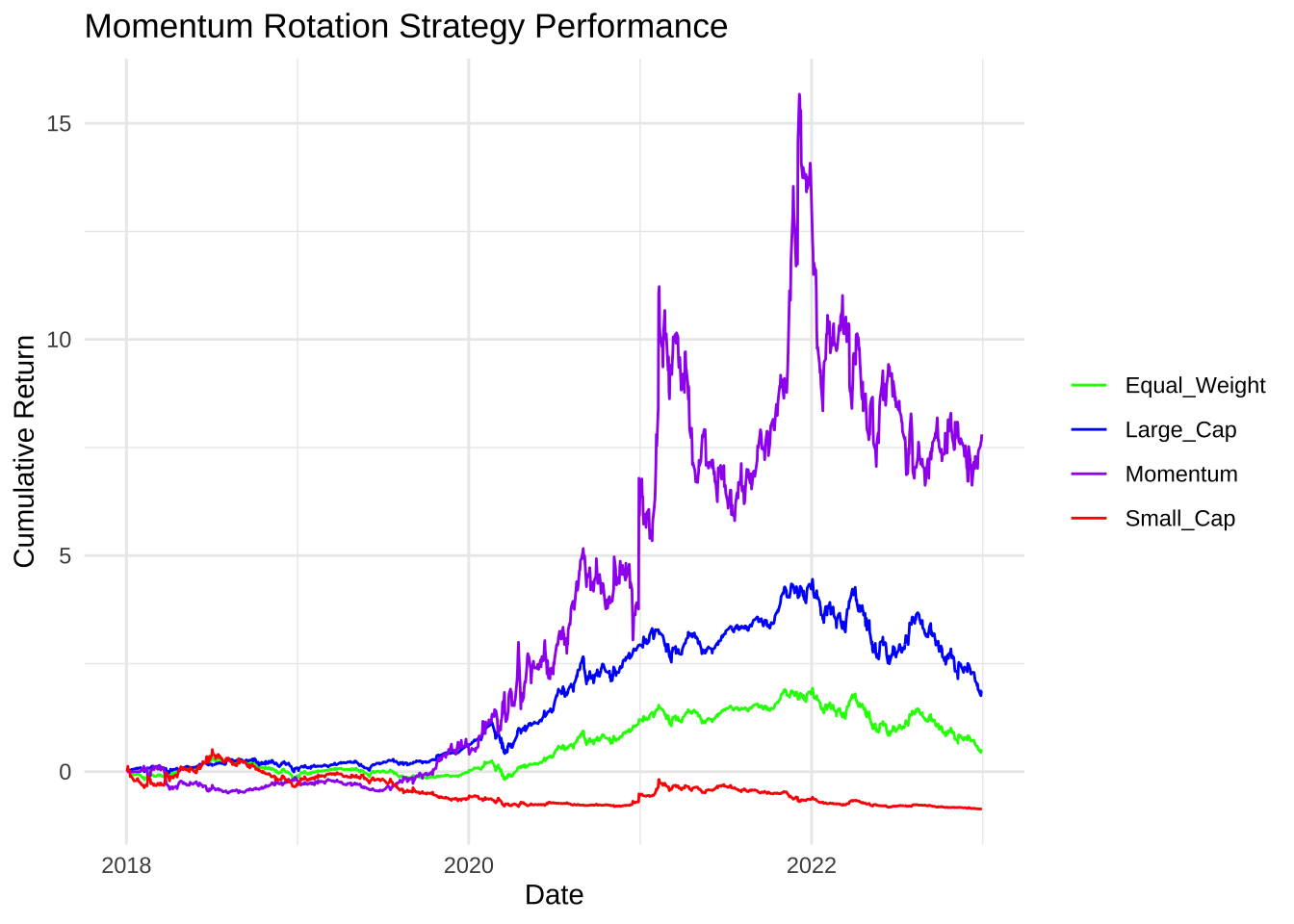
title = "Momentum Rotation Strategy Performance",
x = "Date",
y = "Cumulative Return"
) +
scale_color_manual(values = c(
"Large_Cap" = "blue", "Small_Cap" = "red",
"Equal_Weight" = "green", "Momentum" = "purple"
)) +
theme_minimal() +
theme(legend.title = element_blank())
# 计算策略表现指标
library(PerformanceAnalytics)
performance_metrics <- data.frame(
Strategy = c(
"Large Cap Buy & Hold", "Small Cap Buy & Hold",
"Equal Weight Buy & Hold", "Momentum Rotation"
),
Total_Return = c(
buy_hold_large_cap[length(buy_hold_large_cap)],
buy_hold_small_cap[length(buy_hold_small_cap)],
buy_hold_equal[length(buy_hold_equal)],
strategy_results$xts$Cumulative_Returns[length(strategy_results$xts$Cumulative_Returns)]
),
Sharpe_Ratio = c(
SharpeRatio.annualized(strategy_results$xts$Large_Cap_Returns),
SharpeRatio.annualized(strategy_results$xts$Small_Cap_Returns),
SharpeRatio.annualized((strategy_results$xts$Large_Cap_Returns + strategy_results$xts$Small_Cap_Returns) / 2),
SharpeRatio.annualized(strategy_results$xts$Net_Returns)
),
Max_Drawdown = c(
maxDrawdown(strategy_results$xts$Large_Cap_Returns),
maxDrawdown(strategy_results$xts$Small_Cap_Returns),
maxDrawdown((strategy_results$xts$Large_Cap_Returns + strategy_results$xts$Small_Cap_Returns) / 2),
maxDrawdown(strategy_results$xts$Net_Returns)
)
)
# 展示性能指标
print(performance_metrics)
## Strategy Total_Return Sharpe_Ratio Max_Drawdown
## X2022.12.30 Large Cap Buy & Hold 1.8775824 0.4884327 0.5331828
## X2022.12.30.1 Small Cap Buy & Hold -0.8534490 -0.6581043 0.9683605
## X2022.12.30.2 Equal Weight Buy & Hold 0.5120667 -0.3795699 0.7173901
## X2022.12.30.3 Momentum Rotation 7.8035737 0.3099696 0.6298531
参数优化
接下来,我们将优化动量轮动策略的参数。主要优化的参数是回看期(lookback_period)、 持有期(holding_period)和再平衡阈值(rebalance_threshold)。
我们将使用网格搜索方法来寻找最优参数组合:
# 参数优化主流程
pkg <- c(
"quantmod", "PerformanceAnalytics", "foreach", "doParallel",
"ggplot2", "dplyr", "tidyr", "caret", "magrittr"
)
# 设置参数网格
lookback_periods <- c(5, 10, 20, 30, 60)
holding_periods <- c(5, 10, 20, 30)
rebalance_thresholds <- c(0.01, 0.025, 0.05, 0.1)
# 创建并行集群
cl <- makeCluster(detectCores() - 1)
registerDoParallel(cl)
# 带错误处理的参数优化
optimization_results <- foreach(
lookback = lookback_periods, .combine = rbind,
.packages = pkg, .errorhandling = "pass"
) %:%
foreach(
holding = holding_periods, .combine = rbind,
.packages = pkg
) %:%
foreach(
threshold = rebalance_thresholds, .combine = rbind,
.packages = pkg
) %dopar% {
strategy_result <- momentum_rotation_strategy(
lapply(large_cap_symbols, function(s) stock_data[[s]]),
lapply(small_cap_symbols, function(s) stock_data[[s]]),
lookback, holding, threshold
)
strategy_result_xts <- strategy_result$xts
net_returns <- strategy_result_xts$Net_Returns
sharpe <- as.numeric(SharpeRatio.annualized(net_returns)[1])
data.frame(
Lookback_Period = lookback,
Holding_Period = holding,
Rebalance_Threshold = threshold,
Sharpe_Ratio = sharpe
)
}
stopCluster(cl)
# 结果处理与可视化
optimization_results <- optimization_results[complete.cases(optimization_results), ]
best_params <- optimization_results[which.max(optimization_results$Sharpe_Ratio), ]
print(paste(
"最优参数组合: 回看期=", best_params$Lookback_Period,
" 持有期=", best_params$Holding_Period,
" 阈值=", best_params$Rebalance_Threshold,
" 夏普比率=", round(best_params$Sharpe_Ratio, 3)
))
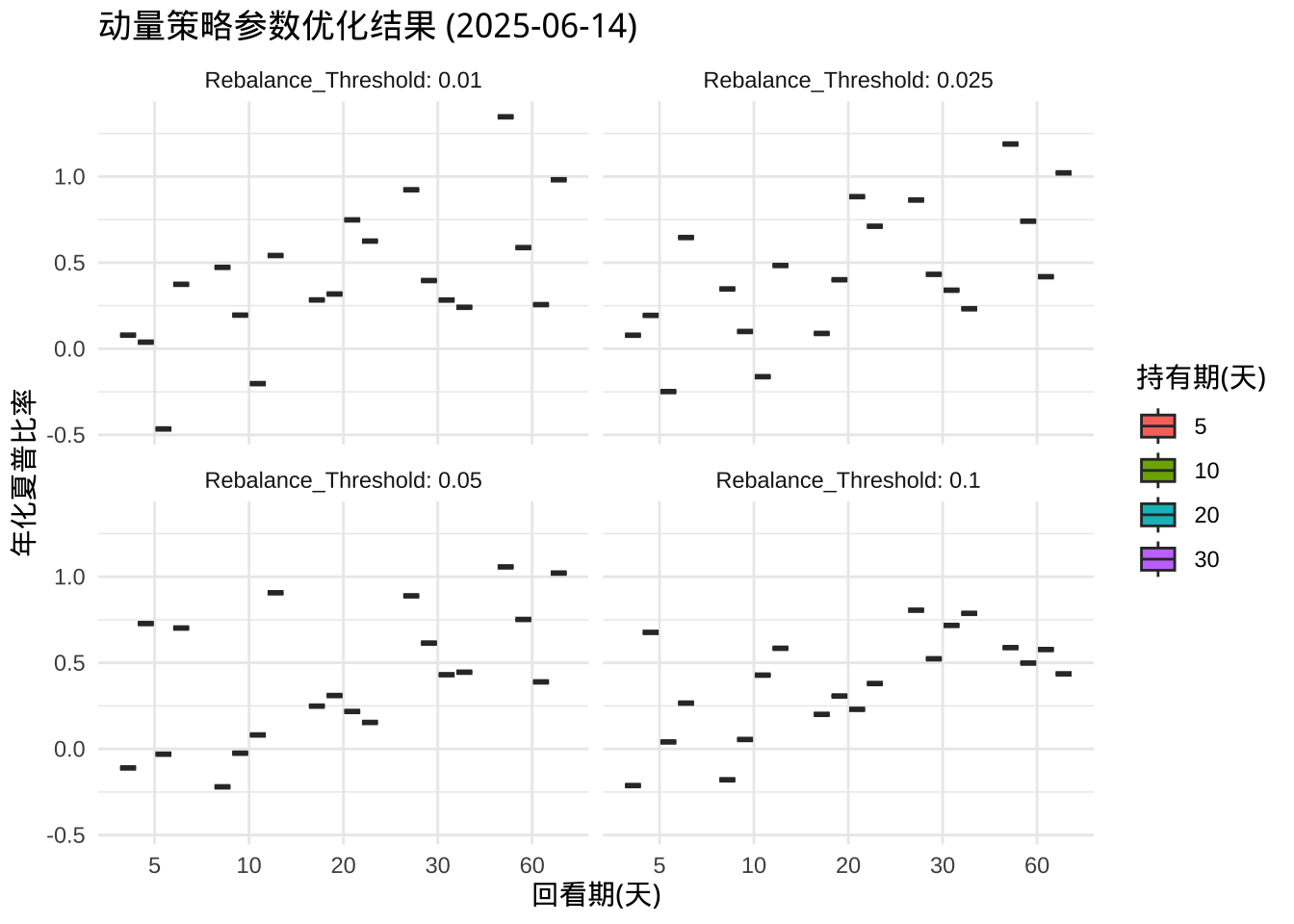
## [1] "最优参数组合: 回看期= 60 持有期= 5 阈值= 0.01 夏普比率= 1.347"
ggplot(
optimization_results,
aes(
x = factor(Lookback_Period), y = Sharpe_Ratio,
fill = factor(Holding_Period)
)
) +
geom_boxplot() +
facet_wrap(~Rebalance_Threshold, labeller = label_both) +
theme_minimal() +
labs(
title = "动量策略参数优化结果 (2025-06-14)",
x = "回看期(天)",
y = "年化夏普比率",
fill = "持有期(天)"
)
参数敏感性分析
为了进一步了解策略对不同参数的敏感性,我们将进行更详细的参数敏感性分析。
# 1. 回看期敏感性分析
# 创建存储结果的数据框结构
lookback_sensitivity <- data.frame(
Lookback_Period = lookback_periods, # 参数测试序列
Sharpe_Ratio = numeric(length(lookback_periods)), # 夏普比率
Total_Return = numeric(length(lookback_periods)), # 总收益
Max_Drawdown = numeric(length(lookback_periods)) # 最大回撤
)
# 遍历测试不同回看期参数
for (i in seq_along(lookback_periods)) {
result <- momentum_rotation_strategy(
lapply(large_cap_symbols, function(s) stock_data[[s]]), # 大盘股数据
lapply(small_cap_symbols, function(s) stock_data[[s]]), # 小盘股数据
lookback_period = lookback_periods[i], # 当前测试的回看期
holding_period = best_params$Holding_Period, # 固定持有期
rebalance_threshold = best_params$Rebalance_Threshold # 固定阈值
)
# 存储绩效指标
lookback_sensitivity$Sharpe_Ratio[i] <- SharpeRatio.annualized(result$xts$Net_Returns)
lookback_sensitivity$Total_Return[i] <- tail(result$xts$Cumulative_Returns, 1)
lookback_sensitivity$Max_Drawdown[i] <- maxDrawdown(result$xts$Net_Returns)
}
# 2. 持有期敏感性分析(结构同上)
holding_sensitivity <- data.frame(
Holding_Period = holding_periods,
Sharpe_Ratio = numeric(length(holding_periods)),
Total_Return = numeric(length(holding_periods)),
Max_Drawdown = numeric(length(holding_periods))
)
for (i in seq_along(holding_periods)) {
result <- momentum_rotation_strategy(
lapply(large_cap_symbols, function(s) stock_data[[s]]),
lapply(small_cap_symbols, function(s) stock_data[[s]]),
lookback_period = best_params$Lookback_Period,
holding_period = holding_periods[i], # 测试不同持有期
rebalance_threshold = best_params$Rebalance_Threshold
)
holding_sensitivity$Sharpe_Ratio[i] <- SharpeRatio.annualized(result$xts$Net_Returns)
holding_sensitivity$Total_Return[i] <- tail(result$xts$Cumulative_Returns, 1)
holding_sensitivity$Max_Drawdown[i] <- maxDrawdown(result$xts$Net_Returns)
}
# 3. 再平衡阈值敏感性分析
threshold_sensitivity <- data.frame(
Rebalance_Threshold = rebalance_thresholds,
Sharpe_Ratio = numeric(length(rebalance_thresholds)),
Total_Return = numeric(length(rebalance_thresholds)),
Max_Drawdown = numeric(length(rebalance_thresholds))
)
for (i in seq_along(rebalance_thresholds)) {
result <- momentum_rotation_strategy(
lapply(large_cap_symbols, function(s) stock_data[[s]]),
lapply(small_cap_symbols, function(s) stock_data[[s]]),
lookback_period = best_params$Lookback_Period,
holding_period = best_params$Holding_Period,
rebalance_threshold = rebalance_thresholds[i] # 测试不同阈值
)
threshold_sensitivity$Sharpe_Ratio[i] <- SharpeRatio.annualized(result$xts$Net_Returns)
threshold_sensitivity$Total_Return[i] <- tail(result$xts$Cumulative_Returns, 1)
threshold_sensitivity$Max_Drawdown[i] <- maxDrawdown(result$xts$Net_Returns)
}
# 4. 可视化分析结果
plot_sensitivity <- function(data, param_name) {
long_data <- data %>%
pivot_longer(
cols = c(Sharpe_Ratio, Total_Return),
names_to = "Metric", values_to = "Value"
)
ggplot(long_data, aes(
x = .data[[names(data)[1]]], y = Value,
color = Metric, group = Metric
)) +
geom_line(linewidth = 1.2) +
geom_point(size = 3) +
labs(
title = paste(param_name, "敏感性分析"),
x = param_name, y = "指标值"
) +
scale_color_manual(
values = c("Sharpe_Ratio" = "#1f77b4", "Total_Return" = "#ff7f0e"),
labels = c("夏普比率", "总收益率")
) +
theme_minimal(base_size = 14) +
theme(legend.position = "bottom")
}
# 生成三个参数的敏感性图表
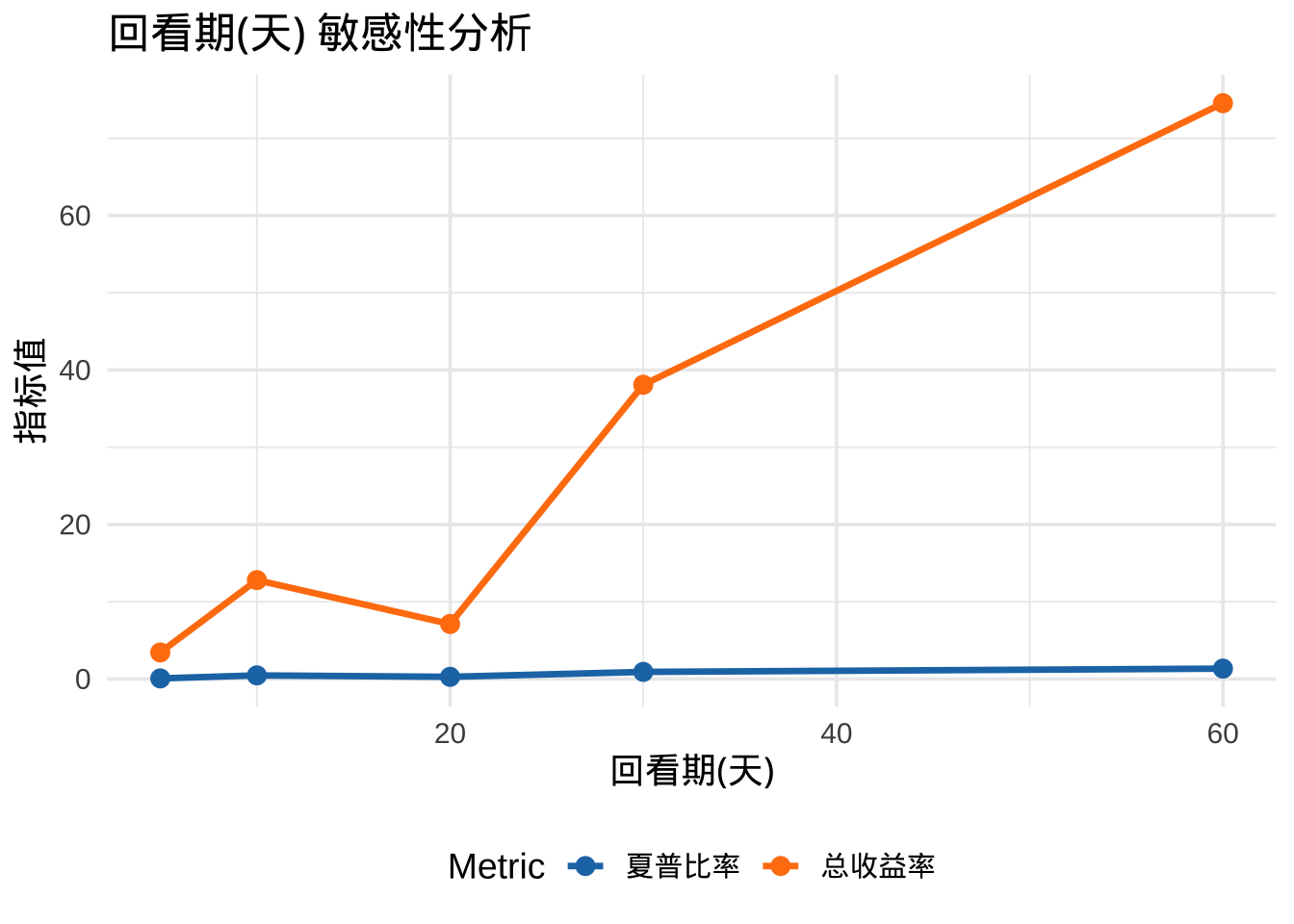
plot_sensitivity(lookback_sensitivity, "回看期(天)")
plot_sensitivity(holding_sensitivity, "持有期(天)")
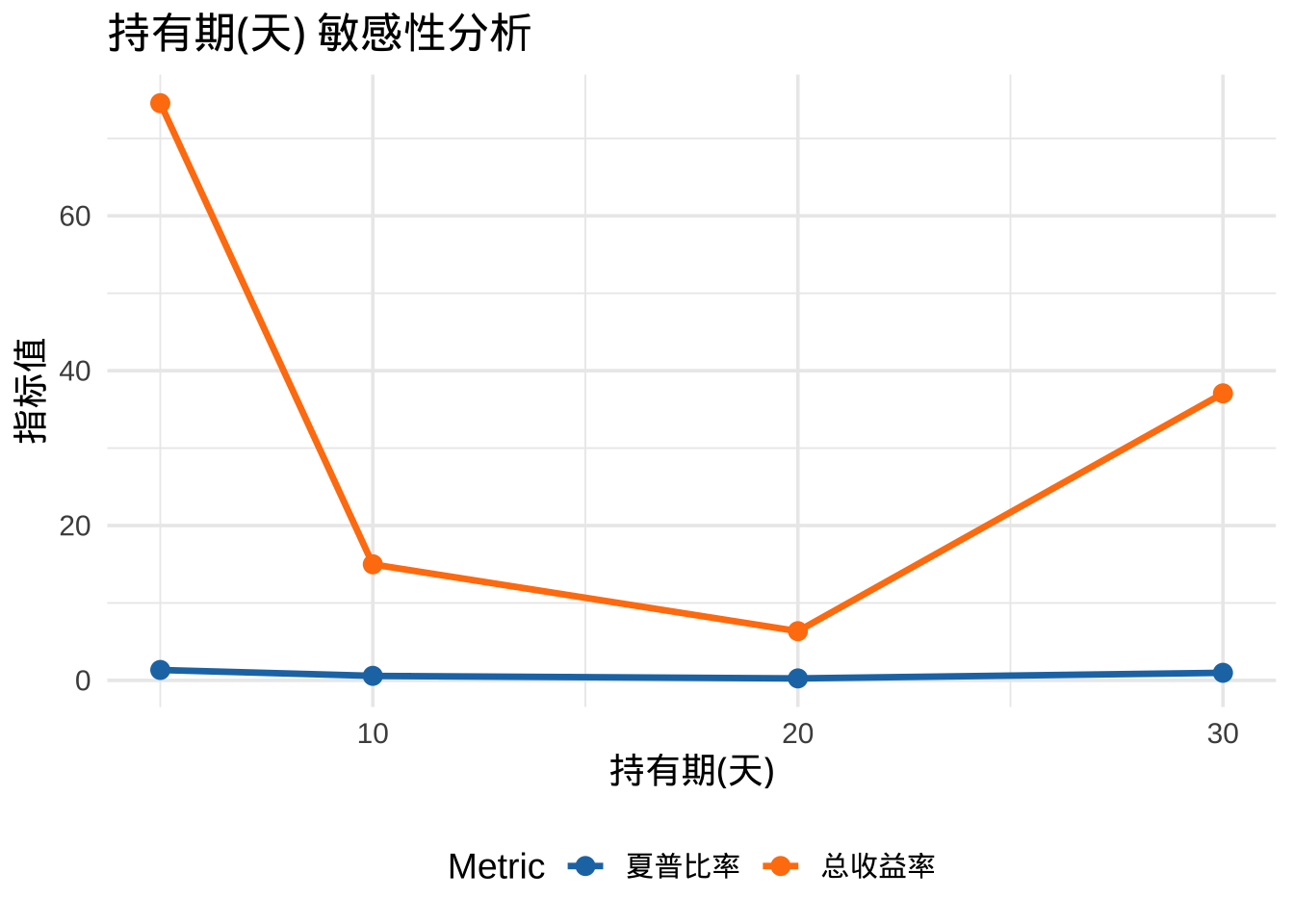
plot_sensitivity(threshold_sensitivity, "再平衡阈值")
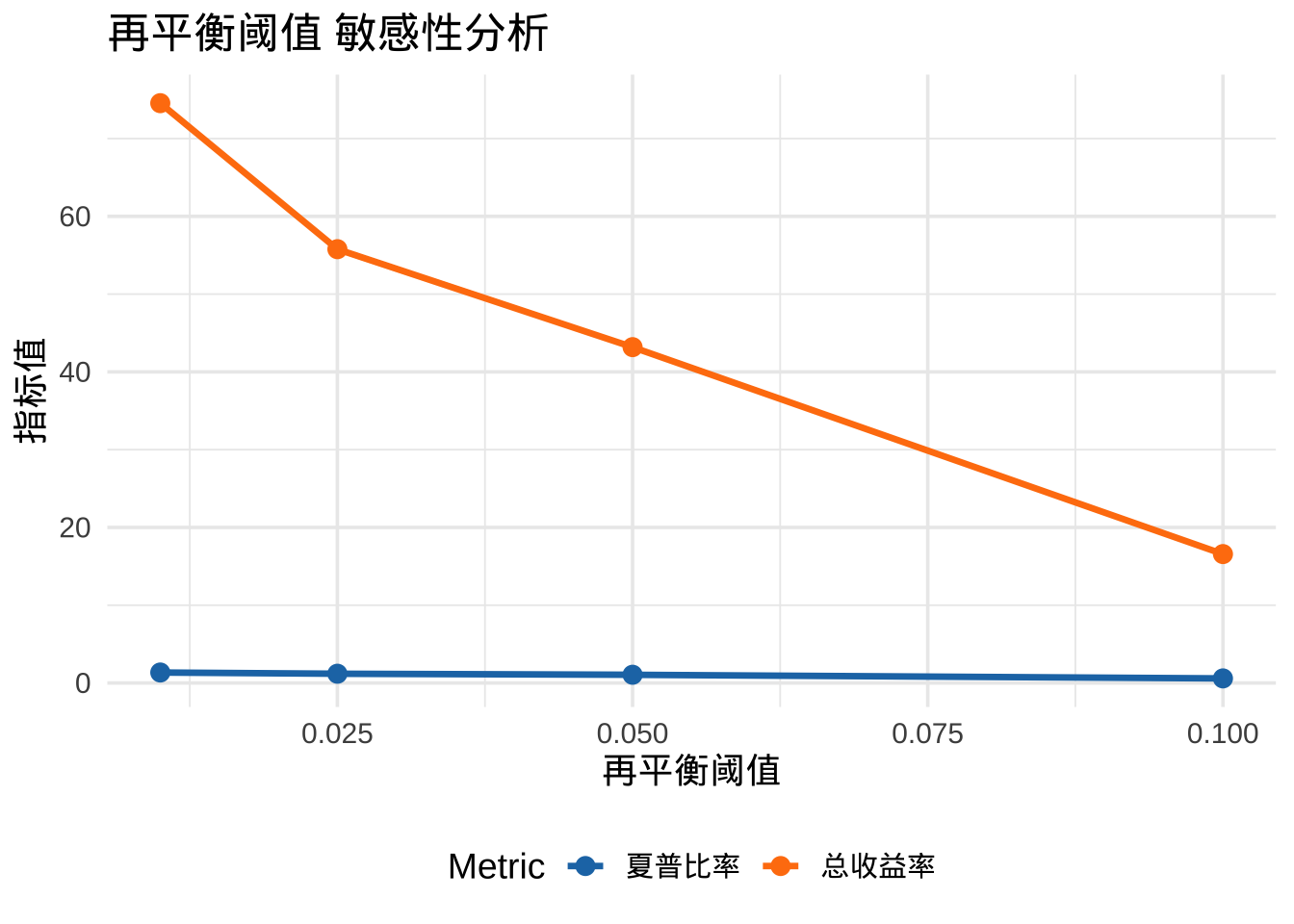
样本外验证
现在我们使用优化后的参数在样本外数据上验证策略的有效性:
# 使用优化后的参数在样本外数据上测试策略
oos_result <- momentum_rotation_strategy(
lapply(large_cap_symbols, function(symbol) oos_data[[symbol]]), # 加载大盘股样本外数据
lapply(small_cap_symbols, function(symbol) oos_data[[symbol]]), # 加载小盘股样本外数据
lookback_period = best_params$Lookback_Period, # 使用优化得到的回看期参数
holding_period = best_params$Holding_Period, # 使用优化得到的持有期参数
rebalance_threshold = best_params$Rebalance_Threshold # 使用优化得到的再平衡阈值
)
# 计算样本外买入持有策略的收益(大盘股)
oos_buy_hold_large_cap <- exp(cumsum(oos_result$xts$Large_Cap_Returns)) - 1 # 累计收益计算
# 计算样本外买入持有策略的收益(小盘股)
oos_buy_hold_small_cap <- exp(cumsum(oos_result$xts$Small_Cap_Returns)) - 1
# 计算等权买入持有策略的收益
oos_buy_hold_equal <- (oos_buy_hold_large_cap + oos_buy_hold_small_cap) / 2
# 准备可视化数据
oos_performance_data <- data.frame(
Date = as.Date(index(oos_result$xts$Large_Cap_Returns)), # 日期序列
Large_Cap = oos_buy_hold_large_cap, # 大盘股买入持有收益
Small_Cap = oos_buy_hold_small_cap, # 小盘股买入持有收益
Equal_Weight = oos_buy_hold_equal, # 等权组合收益
Momentum = oos_result$xts$Cumulative_Returns # 动量策略收益
)
# 转换数据为长格式便于ggplot绘图
oos_performance_data_long <- oos_performance_data %>%
pivot_longer(cols = -Date,
names_to = "Strategy",
values_to = "Cumulative_Return")
# 绘制累积收益对比图
ggplot(oos_performance_data_long,
aes(x = Date,
y = Cumulative_Return, color = Strategy)) +
geom_line() + # 绘制折线图
labs(
title = "样本外策略表现", # 图表标题
x = "Date", y = "Cumulative Return"
) + # 坐标轴标签
scale_color_manual(values = c(
"Large_Cap" = "blue", "Small_Cap" = "red",
"Equal_Weight" = "green", "Momentum" = "purple"
)) + # 颜色设置
theme_minimal() + # 使用简洁主题
theme(legend.title = element_blank()) # 隐藏图例标题
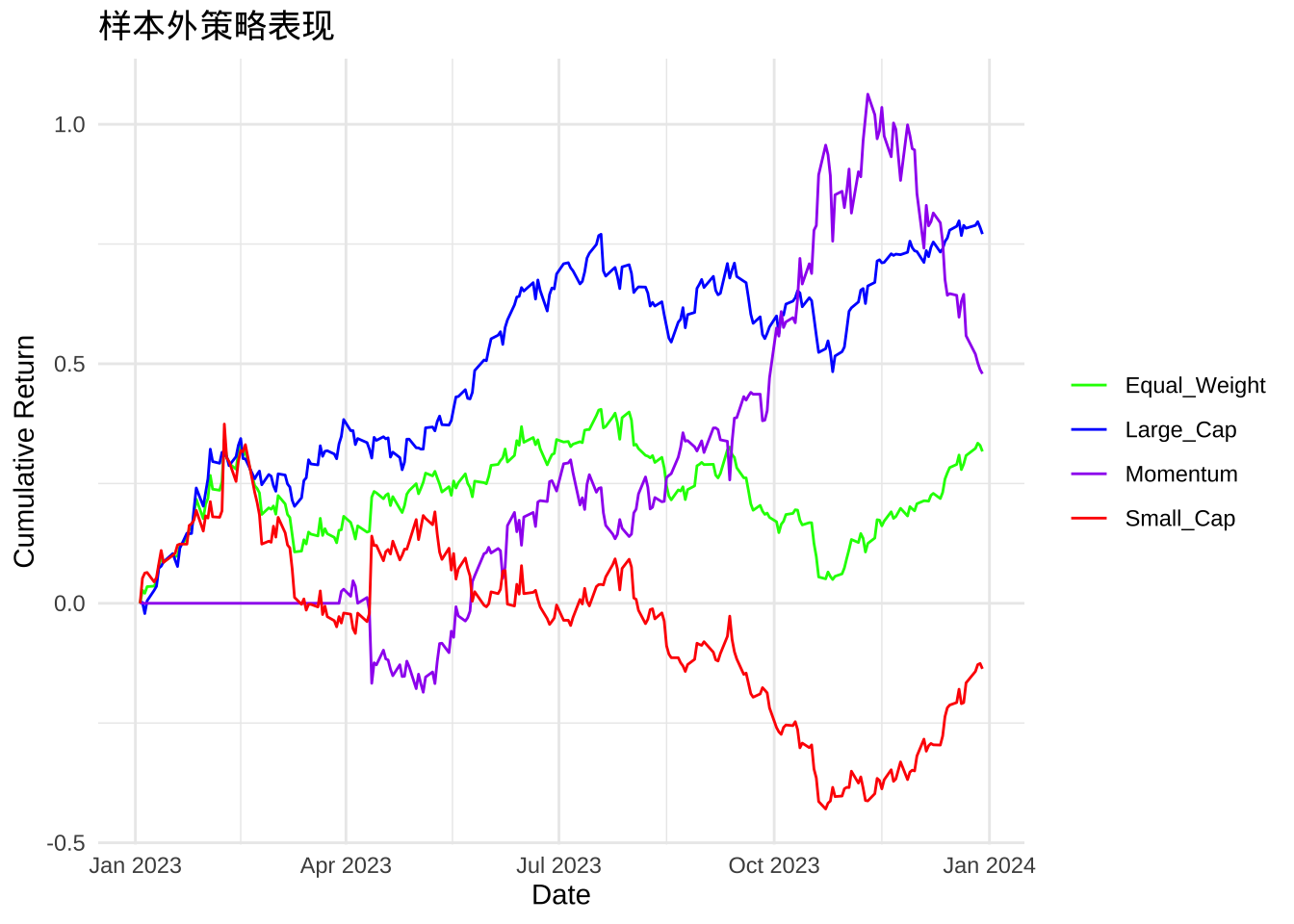
# 计算样本外策略表现指标
oos_performance <- data.frame(
Strategy = c(
"Large Cap Buy & Hold", "Small Cap Buy & Hold",
"Equal Weight Buy & Hold", "Momentum Rotation"
), # 策略名称
Total_Return = c(
oos_buy_hold_large_cap[length(oos_buy_hold_large_cap)], # 大盘股总收益
oos_buy_hold_small_cap[length(oos_buy_hold_small_cap)], # 小盘股总收益
oos_buy_hold_equal[length(oos_buy_hold_equal)], # 等权组合总收益
oos_result$xts$Cumulative_Returns[length(oos_result$xts$Cumulative_Returns)] # 动量策略总收益
),
Sharpe_Ratio = c(
SharpeRatio.annualized(oos_result$xts$Large_Cap_Returns), # 大盘股夏普比率
SharpeRatio.annualized(oos_result$xts$Small_Cap_Returns), # 小盘股夏普比率
SharpeRatio.annualized((oos_result$xts$Large_Cap_Returns + oos_result$xts$Small_Cap_Returns) / 2), # 等权组合夏普比率
SharpeRatio.annualized(oos_result$xts$Net_Returns) # 动量策略夏普比率
),
Max_Drawdown = c(
maxDrawdown(oos_result$xts$Large_Cap_Returns), # 大盘股最大回撤
maxDrawdown(oos_result$xts$Small_Cap_Returns), # 小盘股最大回撤
maxDrawdown((oos_result$xts$Large_Cap_Returns + oos_result$xts$Small_Cap_Returns) / 2), # 等权组合最大回撤
maxDrawdown(oos_result$xts$Net_Returns) # 动量策略最大回撤
)
)
# 打印样本外性能指标
print(oos_performance) # 输出策略比较结果
## Strategy Total_Return Sharpe_Ratio Max_Drawdown
## X2023.12.29 Large Cap Buy & Hold 0.7708001 2.9047901 0.1693780
## X2023.12.29.1 Small Cap Buy & Hold -0.1367801 -0.4796014 0.6159451
## X2023.12.29.2 Equal Weight Buy & Hold 0.3170100 0.6359367 0.3230760
## X2023.12.29.3 Momentum Rotation 0.4791532 0.7933869 0.2934326
结论
本文通过R语言实现了基于动量的大盘股/小盘股轮动策略,并进行了全面的分析。主要发现 如下:
- 动量轮动策略在回测期间表现出了优于简单买入持有策略的潜力,特别是在夏普比率方面。
- 通过参数优化,我们找到了最优的回看期、持有期和再平衡阈值组合,显著提高了策略的 表现。
- 参数敏感性分析表明,策略对回看期和持有期较为敏感,而对再平衡阈值的敏感性相对较 低。
- 样本外验证显示,优化后的策略在新数据上仍具有一定的有效性,但性能通常会有所下降, 这反映了过拟合的风险。
总体而言,基于动量的大盘股/小盘股轮动策略是一种可行的投资方法,但需要谨慎选择参数 并进行充分的样本外验证。在实际应用中,还应考虑交易成本、市场环境变化等因素的影响。
未来的研究可以考虑结合其他指标来改进策略,如波动率指标、市场情绪指标等,或者探索 在不同市场环境下的表现差异。