协整理论与配对交易策略分析
引言
协整理论概述
协整理论是现代计量经济学的重要发展,由Engle和Granger(1987)提出,为非平稳时间序列 分析提供了新的方法。如 果两个或多个非平稳时间序列的线性组合是平稳的,则称这些序列 存在协整关系。协 整关系反映了变量之间的长期均衡关系,即使短期内可能偏离这种均衡, 但长期来看会趋向于回归均衡状态。
在金融市场中,许多资产价格序列表现出非平稳性(通常为I(1)过程),但某些资产对之间 可能存在协整关系。这 种协整关系为配对交易策略提供了理论基础。
配对交易策略
配对交易是一种市场中性策略,通过同时买入一只被低估的股票和卖出一只被高估的股票, 从两者价格回归均衡的过程中获利。传 统的配对交易策略通常基于统计套利思想,寻找价格 走势相似的股票对。而 基于协整理论的配对交易则更进一步,不仅要求价格走势相似,还要 求存在长期稳定的均衡关系。
配对交易策略的优势在于:
- 市场中性:不受整体市场涨跌影响
- 风险分散:同时持有多头和空头头寸
- 统计基础:基于严格的统计理论
- 可量化:策略参数和交易信号明确
本文将通过实证分析,展示如何应用协整理论构建和评估配对交易策略。
理论基础
单位根检验
在进行协整分析之前,需要先检验时间序列是否存在单位根,即是否为非平稳序列。常 用的 单位根检验方法包括:
ADF检验(增广迪基-富勒检验)
ADF检验的原假设为序列存在单位根(非平稳),备择假设为序列不存在单位根(平稳)。检 验统计量为:
$$ \Delta y_{t} = \alpha + \beta t + \gamma y_{t-1} + \sum_{i=1}^{p} \delta_{i} \Delta y_{t-i} +\varepsilon_{t} $$
其中,$\gamma=0$ 表示存在单位根。
KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin检验)
KPSS检验与ADF检验相反,其原假设为序列是平稳的,备择假设为序列存在单位根。
协整检验
在确认两个序列均为非平稳序列后,需要检验它们是否存在协整关系。常 用的协整检验方法 包括:
Engle-Granger两步法
Engle-Granger两步法的步骤如下:
- 对两个非平稳序列进行线性回归:$y_{t} = \alpha + \beta x_{t} + \varepsilon_{t}$
- 检验回归残差序列$\hat{\varepsilon}_{t}$ 是否平稳
- 如果残差序列平稳,则两个序列存在协整关系
Johansen检验
Johansen检验是一种多变量协整检验方法,适用于检验多个时间序列之间的协整关系。它 基 于向量自回归模型(VAR),通过最大似然估计法估计协整向量。
误差修正模型(ECM)
如果两个序列存在协整关系,则可以建立误差修正模型来描述它们的短期动态关系。误 差修 正模型的一般形式为:
$$ \Delta y_{t} = \alpha_{1} + \sum_{i=1}^{p} \beta_{1i} \Delta y_{t-i} + \sum_{i=0}^{q} \gamma_{1i} \Delta x_{t-i} + \lambda_{1} (y_{t-1} - \beta x_{t-1}) + \varepsilon_{1t} $$
$$ \Delta x_{t}=\alpha_{2}+\sum_{i=1}^{p}\beta_{2i}\Delta x_{t-i}+\sum_{i=0}^{q}\gamma_{2i}\Delta y_{t-i}+\lambda_{2}(y_{t-1}-\beta x_{t-1})+\varepsilon_{2t} $$
其中,$(y_{t-1}-\beta x_{t-1})$ 是误差修正项,表示对长期均衡关系的偏离。
实证分析
数据获取与预处理
首先加载所需的R包并获取股票数据:
# 加载必要的R包
library(quantmod) # 获取金融数据
library(tseries) # 时间序列分析
library(urca) # 单位根和协整检验
library(ggplot2) # 数据可视化
library(dplyr) # 数据处理
library(PerformanceAnalytics) # 绩效分析
library(knitr) # 表格输出
设置时间范围并获取股票数据:
# 设置时间范围
start_date <- "2018-01-01"
end_date <- "2023-01-01"
# 定义股票代码 - 以美国大型科技股为例
tickers <- c("AAPL", "MSFT", "AMZN", "GOOGL", "META", "NFLX", "TSLA", "NVDA")
# 创建一个空列表存储股票数据
stock_data <- list()
# 获取每只股票的价格数据
for(ticker in tickers) {
stock_data[[ticker]] <- getSymbols(ticker, from = start_date, to = end_date, auto.assign = FALSE)
}
# 提取收盘价并合并为一个数据框
close_prices <- do.call(merge, lapply(stock_data, Cl))
colnames(close_prices) <- tickers
# 查看数据基本信息
str(close_prices)
## An xts object on 2018-01-02 / 2022-12-30 containing:
## Data: double [1259, 8]
## Columns: AAPL, MSFT, AMZN, GOOGL, META ... with 3 more columns
## Index: Date [1259] (TZ: "UTC")
## xts Attributes:
## $ src : chr "yahoo"
## $ updated: POSIXct[1:1], format: "2025-07-03 08:40:52"
summary(close_prices)
## Index AAPL MSFT AMZN
## Min. :2018-01-02 Min. : 35.55 Min. : 85.01 Min. : 59.45
## 1st Qu.:2019-04-03 1st Qu.: 51.02 1st Qu.:119.60 1st Qu.: 88.93
## Median :2020-07-02 Median : 91.63 Median :201.91 Median :107.78
## Mean :2020-07-02 Mean : 98.09 Mean :193.87 Mean :119.81
## 3rd Qu.:2021-09-30 3rd Qu.:142.86 3rd Qu.:255.25 3rd Qu.:158.09
## Max. :2022-12-30 Max. :182.01 Max. :343.11 Max. :186.57
## GOOGL META NFLX TSLA
## Min. : 49.23 Min. : 88.91 Min. :166.4 Min. : 11.93
## 1st Qu.: 58.74 1st Qu.:170.53 1st Qu.:298.6 1st Qu.: 21.08
## Median : 73.96 Median :194.47 Median :361.8 Median : 80.58
## Mean : 85.71 Mean :217.89 Mean :387.8 Mean :131.78
## 3rd Qu.:112.67 3rd Qu.:266.87 3rd Qu.:494.5 3rd Qu.:236.12
## Max. :149.84 Max. :382.18 Max. :691.7 Max. :409.97
## NVDA
## Min. : 3.177
## 1st Qu.: 5.606
## Median : 9.612
## Mean :11.629
## 3rd Qu.:16.146
## Max. :33.376
绘制价格走势图:
# 绘制价格走势图
price_df <- data.frame(
date = index(close_prices),
close_prices
)
price_long <- reshape2::melt(price_df, id.vars = "date")
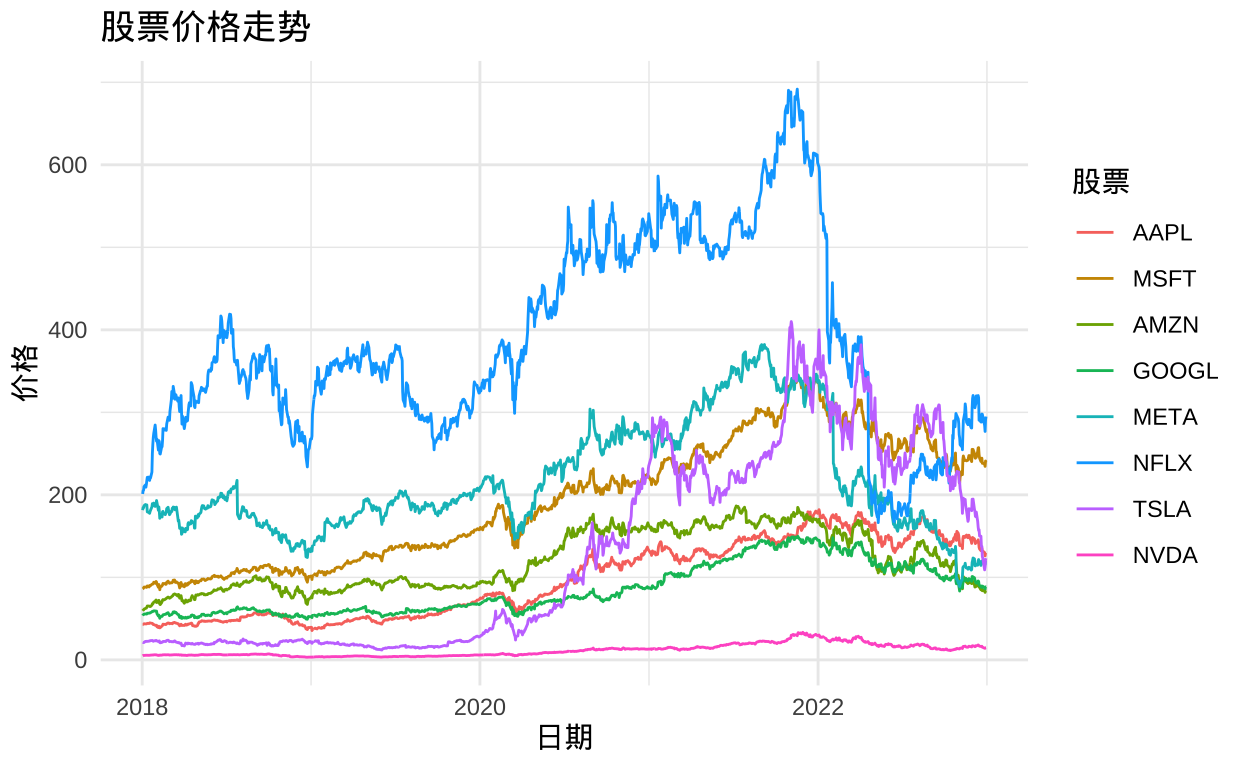
ggplot(price_long, aes(x = date, y = value, color = variable)) +
geom_line() +
labs(title = "股票价格走势",
x = "日期",
y = "价格",
color = "股票") +
theme_minimal()
单位根检验
对每只股票的价格序列进行单位根检验,确认其非平稳性:
# 创建一个函数进行ADF检验
perform_adf_test <- function(series) {
adf_result <- adf.test(series)
return(data.frame(
Statistic = adf_result$statistic,
P_Value = adf_result$p.value,
Stationary = ifelse(adf_result$p.value < 0.05, "是", "否")
))
}
# 对每只股票进行ADF检验
adf_results <- lapply(close_prices, perform_adf_test)
adf_results_df <- do.call(rbind, adf_results)
rownames(adf_results_df) <- tickers
# 展示ADF检验结果
knitr::kable(adf_results_df,
caption = "股票价格序列的ADF单位根检验结果",
digits = 4,
booktabs = TRUE)
Table: (#tab:adf_test)股票价格序列的ADF单位根检验结果
| Statistic | P_Value | Stationary | |
|---|---|---|---|
| AAPL | -1.5667 | 0.7617 | 否 |
| MSFT | -1.1554 | 0.9137 | 否 |
| AMZN | -0.4665 | 0.9833 | 否 |
| GOOGL | -0.6337 | 0.9757 | 否 |
| META | -0.4532 | 0.9839 | 否 |
| NFLX | -1.5389 | 0.7735 | 否 |
| TSLA | -1.2537 | 0.8942 | 否 |
| NVDA | -1.7233 | 0.6954 | 否 |
# 对价格取对数并差分,创建收益率序列
returns <- diff(log(close_prices))[-1]
# 对收益率序列进行ADF检验
returns_adf_results <- lapply(returns, perform_adf_test)
returns_adf_results_df <- do.call(rbind, returns_adf_results)
rownames(returns_adf_results_df) <- tickers
# 展示收益率序列的ADF检验结果
knitr::kable(returns_adf_results_df,
caption = "股票收益率序列的ADF单位根检验结果",
digits = 4,
booktabs = TRUE)
Table: (#tab:adf_test)股票收益率序列的ADF单位根检验结果
| Statistic | P_Value | Stationary | |
|---|---|---|---|
| AAPL | -10.2580 | 0.01 | 是 |
| MSFT | -11.6003 | 0.01 | 是 |
| AMZN | -11.4524 | 0.01 | 是 |
| GOOGL | -11.2531 | 0.01 | 是 |
| META | -11.6074 | 0.01 | 是 |
| NFLX | -10.9801 | 0.01 | 是 |
| TSLA | -9.9687 | 0.01 | 是 |
| NVDA | -10.4041 | 0.01 | 是 |
寻找潜在的协整对
计算股票之间的相关性,并寻找可能存在协整关系的股票对:
# 计算价格序列的相关性矩阵
correlation_matrix <- cor(close_prices, use = "complete.obs")
# 展示相关性矩阵
knitr::kable(correlation_matrix,
caption = "股票价格序列相关性矩阵",
digits = 4,
booktabs = TRUE)
Table: (#tab:correlation_analysis)股票价格序列相关性矩阵
| AAPL | MSFT | AMZN | GOOGL | META | NFLX | TSLA | NVDA | |
|---|---|---|---|---|---|---|---|---|
| AAPL | 1.0000 | 0.9722 | 0.8029 | 0.9316 | 0.5147 | 0.3635 | 0.9618 | 0.9228 |
| MSFT | 0.9722 | 1.0000 | 0.8451 | 0.9611 | 0.6168 | 0.4685 | 0.9439 | 0.9411 |
| AMZN | 0.8029 | 0.8451 | 1.0000 | 0.8044 | 0.8391 | 0.7683 | 0.7974 | 0.7960 |
| GOOGL | 0.9316 | 0.9611 | 0.8044 | 1.0000 | 0.6528 | 0.4616 | 0.9418 | 0.9594 |
| META | 0.5147 | 0.6168 | 0.8391 | 0.6528 | 1.0000 | 0.8551 | 0.5404 | 0.6216 |
| NFLX | 0.3635 | 0.4685 | 0.7683 | 0.4616 | 0.8551 | 1.0000 | 0.4042 | 0.4922 |
| TSLA | 0.9618 | 0.9439 | 0.7974 | 0.9418 | 0.5404 | 0.4042 | 1.0000 | 0.9357 |
| NVDA | 0.9228 | 0.9411 | 0.7960 | 0.9594 | 0.6216 | 0.4922 | 0.9357 | 1.0000 |
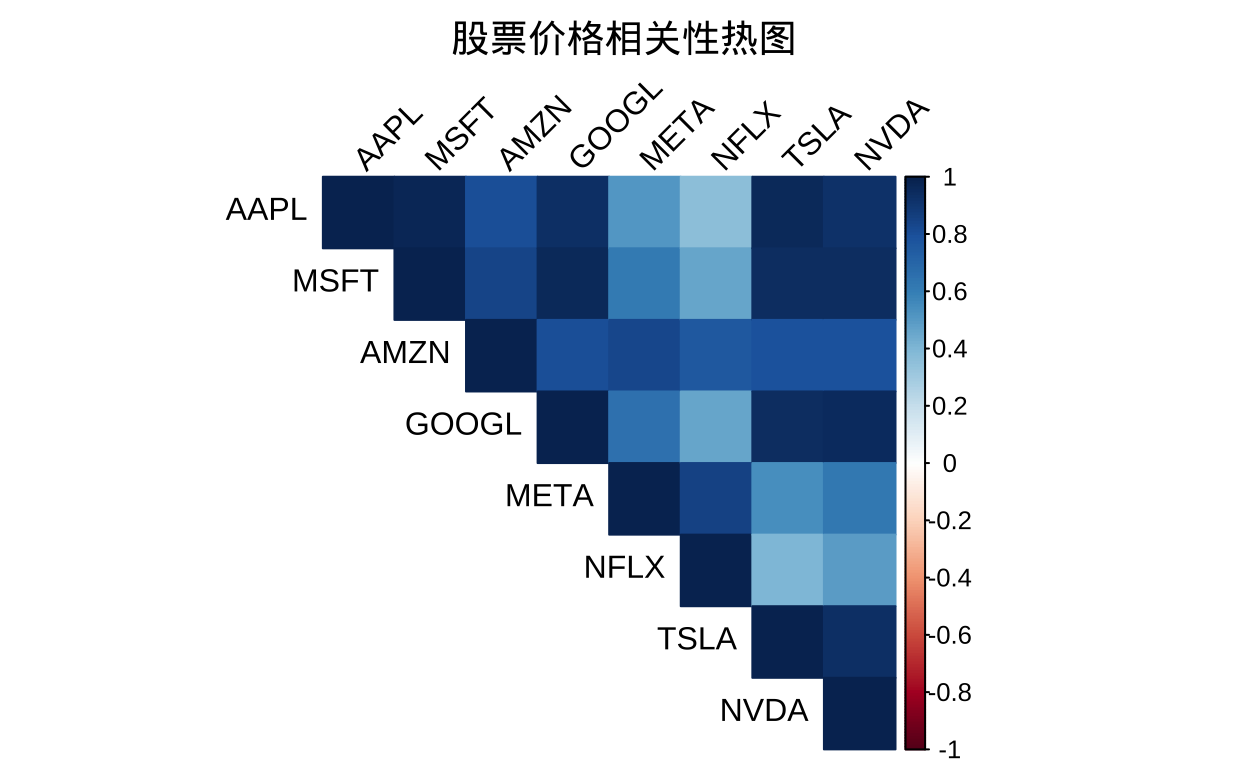
# 绘制相关性热图
library(corrplot)
corrplot(correlation_matrix, method = "color", type = "upper",
tl.col = "black", tl.srt = 45,
title = "股票价格相关性热图", mar = c(0, 0, 2, 0))
# 寻找相关性较高的股票对
high_corr_pairs <- which(correlation_matrix > 0.8 & correlation_matrix < 1, arr.ind = TRUE)
high_corr_pairs <- high_corr_pairs[high_corr_pairs[,1] < high_corr_pairs[,2], ]
# 展示高相关性股票对
high_corr_pairs_df <- data.frame(
Stock1 = rownames(correlation_matrix)[high_corr_pairs[,1]],
Stock2 = rownames(correlation_matrix)[high_corr_pairs[,2]],
Correlation = correlation_matrix[high_corr_pairs]
)
knitr::kable(high_corr_pairs_df,
caption = "相关性较高的股票对",
digits = 4,
booktabs = TRUE)
Table: (#tab:correlation_analysis)相关性较高的股票对
| Stock1 | Stock2 | Correlation |
|---|---|---|
| AAPL | MSFT | 0.9722 |
| AAPL | AMZN | 0.8029 |
| MSFT | AMZN | 0.8451 |
| AAPL | GOOGL | 0.9316 |
| MSFT | GOOGL | 0.9611 |
| AMZN | GOOGL | 0.8044 |
| AMZN | META | 0.8391 |
| META | NFLX | 0.8551 |
| AAPL | TSLA | 0.9618 |
| MSFT | TSLA | 0.9439 |
| GOOGL | TSLA | 0.9418 |
| AAPL | NVDA | 0.9228 |
| MSFT | NVDA | 0.9411 |
| GOOGL | NVDA | 0.9594 |
| TSLA | NVDA | 0.9357 |
协整检验
对相关性较高的股票对进行协整检验:
# 创建一个函数进行Engle-Granger协整检验
perform_eg_test <- function(series1, series2) {
# 第一步:进行线性回归
lm_model <- lm(series1 ~ series2)
# 第二步:获取残差
residuals <- lm_model$residuals
# 第三步:对残差进行ADF检验
adf_result <- adf.test(residuals)
return(list(
lm_model = lm_model,
adf_result = adf_result,
is_cointegrated = adf_result$p.value < 0.05,
beta = coef(lm_model)[2],
alpha = coef(lm_model)[1],
residuals = residuals
))
}
# 对每对高相关性股票进行协整检验
cointegration_results <- list()
for(i in 1:nrow(high_corr_pairs_df)) {
stock1 <- high_corr_pairs_df$Stock1[i]
stock2 <- high_corr_pairs_df$Stock2[i]
result <- perform_eg_test(close_prices[, stock1], close_prices[, stock2])
cointegration_results[[paste(stock1, stock2, sep = "-")]] <- list(
stock1 = stock1,
stock2 = stock2,
p_value = result$adf_result$p.value,
is_cointegrated = result$is_cointegrated,
beta = result$beta,
alpha = result$alpha,
residuals = result$residuals
)
}
# 提取协整检验结果
cointegration_summary <- data.frame(
Pair = names(cointegration_results),
P_Value = sapply(cointegration_results, function(x) x$p_value),
Is_Cointegrated = sapply(cointegration_results, function(x) x$is_cointegrated),
Beta = sapply(cointegration_results, function(x) x$beta),
Alpha = sapply(cointegration_results, function(x) x$alpha)
)
# 展示协整检验结果
knitr::kable(cointegration_summary,
caption = "股票对的协整检验结果",
digits = 4,
booktabs = TRUE)
Table: (#tab:cointegration_test)股票对的协整检验结果
| Pair | P_Value | Is_Cointegrated | Beta | Alpha | |
|---|---|---|---|---|---|
| AAPL-MSFT | AAPL-MSFT | 0.3291 | FALSE | 0.6034 | -18.8900 |
| AAPL-AMZN | AAPL-AMZN | 0.7377 | FALSE | 1.0447 | -27.0757 |
| MSFT-AMZN | MSFT-AMZN | 0.8092 | FALSE | 1.7716 | -18.3808 |
| AAPL-GOOGL | AAPL-GOOGL | 0.5481 | FALSE | 1.4035 | -22.2048 |
| MSFT-GOOGL | MSFT-GOOGL | 0.6072 | FALSE | 2.3331 | -6.0949 |
| AMZN-GOOGL | AMZN-GOOGL | 0.7852 | FALSE | 0.9315 | 39.9734 |
| AMZN-META | AMZN-META | 0.0442 | TRUE | 0.4463 | 22.5573 |
| META-NFLX | META-NFLX | 0.2425 | FALSE | 0.4793 | 32.0470 |
| AAPL-TSLA | AAPL-TSLA | 0.0717 | FALSE | 0.3780 | 48.2774 |
| MSFT-TSLA | MSFT-TSLA | 0.2255 | FALSE | 0.5977 | 115.1065 |
| GOOGL-TSLA | GOOGL-TSLA | 0.0940 | FALSE | 0.2457 | 53.3358 |
| AAPL-NVDA | AAPL-NVDA | 0.2053 | FALSE | 5.8621 | 29.9229 |
| MSFT-NVDA | MSFT-NVDA | 0.3136 | FALSE | 9.6320 | 81.8640 |
| GOOGL-NVDA | GOOGL-NVDA | 0.0757 | FALSE | 4.0452 | 38.6694 |
| TSLA-NVDA | TSLA-NVDA | 0.0916 | FALSE | 15.1244 | -44.0953 |
# 找出存在协整关系的股票对
cointegrated_pairs <- cointegration_summary[cointegration_summary$Is_Cointegrated, ]
# 展示存在协整关系的股票对
if(nrow(cointegrated_pairs) > 0) {
knitr::kable(cointegrated_pairs,
caption = "存在协整关系的股票对",
digits = 4,
booktabs = TRUE)
} else {
print("未找到存在协整关系的股票对")
}
Table: (#tab:cointegration_test)存在协整关系的股票对
| Pair | P_Value | Is_Cointegrated | Beta | Alpha | |
|---|---|---|---|---|---|
| AMZN-META | AMZN-META | 0.0442 | TRUE | 0.4463 | 22.5573 |
可视化协整关系
选择一个存在协整关系的股票对,可视化其价格走势和协整残差:
# 如果存在协整对,选择第一个进行可视化
if(nrow(cointegrated_pairs) > 0) {
selected_pair <- cointegrated_pairs$Pair[1]
stock1 <- cointegration_results[[selected_pair]]$stock1
stock2 <- cointegration_results[[selected_pair]]$stock2
# 绘制价格走势图
price_df <- data.frame(
date = index(close_prices),
Stock1 = close_prices[, stock1],
Stock2 = close_prices[, stock2],
row.names = NULL, # 明确指定没有行名
stringsAsFactors = FALSE # 避免因子转换警告
)
price_long <- reshape2::melt(price_df, id.vars = "date")
ggplot(price_long, aes(x = date, y = value, color = variable)) +
geom_line() +
labs(title = paste(stock1, "和", stock2, "的价格走势"),
x = "日期",
y = "价格",
color = "股票") +
theme_minimal()
# 绘制标准化后的价格走势(便于比较)
normalized_prices <- data.frame(
date = index(close_prices),
Stock1 = close_prices[, stock1] / close_prices[1, stock1],
Stock2 = close_prices[, stock2] / close_prices[1, stock2],
row.names = NULL, # 明确指定没有行名
stringsAsFactors = FALSE # 避免因子转换警告
)
normalized_long <- reshape2::melt(normalized_prices, id.vars = "date")
ggplot(normalized_long, aes(x = date, y = value, color = variable)) +
geom_line() +
labs(title = paste(stock1, "和", stock2, "的标准化价格走势"),
x = "日期",
y = "标准化价格",
color = "股票") +
theme_minimal()
# 绘制协整残差图
residuals <- cointegration_results[[selected_pair]]$residuals
# 确保日期和残差长度一致
date_index <- index(close_prices)
if(length(residuals) < length(date_index)) {
date_index <- date_index[-1]
}
if(length(residuals) > length(date_index)) {
residuals <- residuals[-length(residuals)]
}
residuals_df <- data.frame(
date = date_index,
residual = residuals,
row.names = NULL, # 明确指定没有行名
stringsAsFactors = FALSE # 避免因子转换警告
)
ggplot(residuals_df, aes(x = date, y = residual)) +
geom_line() +
geom_hline(yintercept = 0, color = "red", linetype = "dashed") +
labs(title = paste(stock1, "和", stock2, "的协整残差"),
x = "日期",
y = "残差") +
theme_minimal()
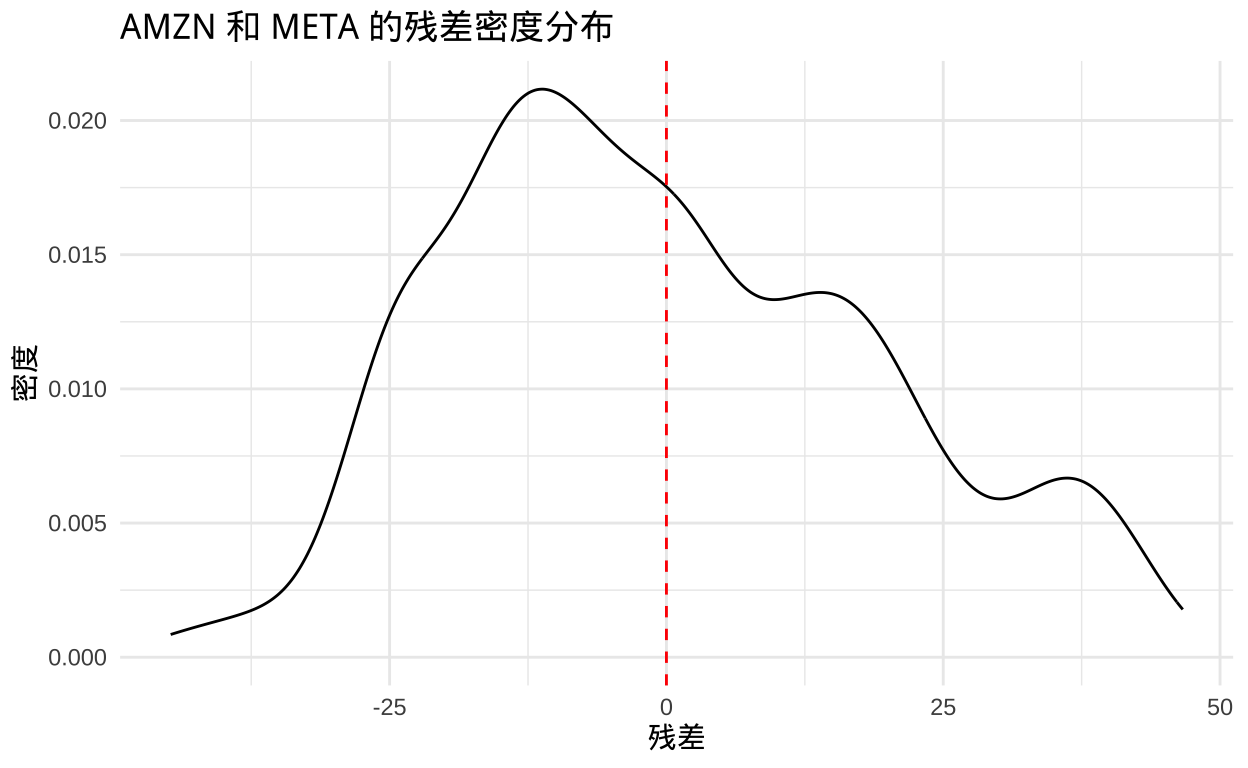
# 绘制残差的密度图
ggplot(residuals_df, aes(x = residual)) +
geom_density() +
geom_vline(xintercept = 0, color = "red", linetype = "dashed") +
labs(title = paste(stock1, "和", stock2, "的残差密度分布"),
x = "残差",
y = "密度") +
theme_minimal()
}
构建配对交易策略
基于协整残差构建配对交易策略:
# 如果存在协整对,构建配对交易策略
if(nrow(cointegrated_pairs) > 0) {
selected_pair <- cointegrated_pairs$Pair[1]
stock1 <- cointegration_results[[selected_pair]]$stock1
stock2 <- cointegration_results[[selected_pair]]$stock2
beta <- cointegration_results[[selected_pair]]$beta
residuals <- cointegration_results[[selected_pair]]$residuals
# 计算残差的均值和标准差
mean_residual <- mean(residuals)
sd_residual <- sd(residuals)
# 设置交易阈值(以标准差为单位)
entry_threshold <- 2
exit_threshold <- 0.5
# 确保日期和残差长度一致
date_index <- index(close_prices)
if(length(residuals) < length(date_index)) {
date_index <- date_index[-1] # 移除第一个日期
} else if(length(residuals) > length(date_index)) {
residuals <- residuals[-length(residuals)] # 移除最后一个残差
}
# 创建交易信号
signals <- data.frame(
date = date_index,
residual = residuals,
signal = 0,
row.names = NULL, # 明确指定不使用行名
stringsAsFactors = FALSE # 防止字符串自动转换为因子
)
# 生成交易信号
# 1: 做多stock1,做空stock2
# -1: 做空stock1,做多stock2
# 0: 不持仓
for(i in 1:nrow(signals)) {
if(signals$residual[i] > mean_residual + entry_threshold * sd_residual) {
signals$signal[i] <- -1 # 残差过高,stock1被高估,stock2被低估
} else if(signals$residual[i] < mean_residual - entry_threshold * sd_residual) {
signals$signal[i] <- 1 # 残差过低,stock1被低估,stock2被高估
} else if(abs(signals$residual[i] - mean_residual) < exit_threshold * sd_residual) {
signals$signal[i] <- 0 # 残差接近均值,平仓
} else {
# 保持前一天的信号
if(i > 1) {
signals$signal[i] <- signals$signal[i-1]
}
}
}
# 计算持仓变化
positions <- signals
positions$position <- c(0, diff(positions$signal))
# 计算收益率
stock1_returns <- diff(log(close_prices[, stock1]))
stock2_returns <- diff(log(close_prices[, stock2]))
# 确保收益率长度与信号长度匹配
# 移除收益率序列中多余的元素
min_length <- min(length(stock1_returns), length(stock2_returns), nrow(signals) - 1)
stock1_returns <- stock1_returns[1:min_length]
stock2_returns <- stock2_returns[1:min_length]
# 确保信号和持仓长度与收益率匹配
# 移除第一个日期对应的信号和持仓(因为没有对应的收益率)
signal_values <- signals$signal[2:(min_length + 1)]
position_values <- positions$position[2:(min_length + 1)]
# 计算策略收益率
strategy_returns <- data.frame(
date = signals$date[2:(min_length + 1)], # 使用调整后的日期
stock1_returns = stock1_returns,
stock2_returns = stock2_returns,
signal = signal_values,
position = position_values,
row.names = NULL, # 明确指定不使用行名
stringsAsFactors = FALSE # 防止字符串自动转换为因子
)
colnames(strategy_returns) <- c("date", "stock1_returns", "stock2_returns", "signal", "position")
# 计算每日策略收益
strategy_returns$daily_return <- strategy_returns$signal * (strategy_returns$stock1_returns - beta * strategy_returns$stock2_returns)
# 计算累计收益
strategy_returns$cumulative_return <- cumsum(strategy_returns$daily_return)
# 可视化策略表现
ggplot(strategy_returns, aes(x = date, y = cumulative_return)) +
geom_line() +
labs(title = paste(stock1, "和", stock2, "的配对交易策略累计收益"),
x = "日期",
y = "累计收益") +
theme_minimal()
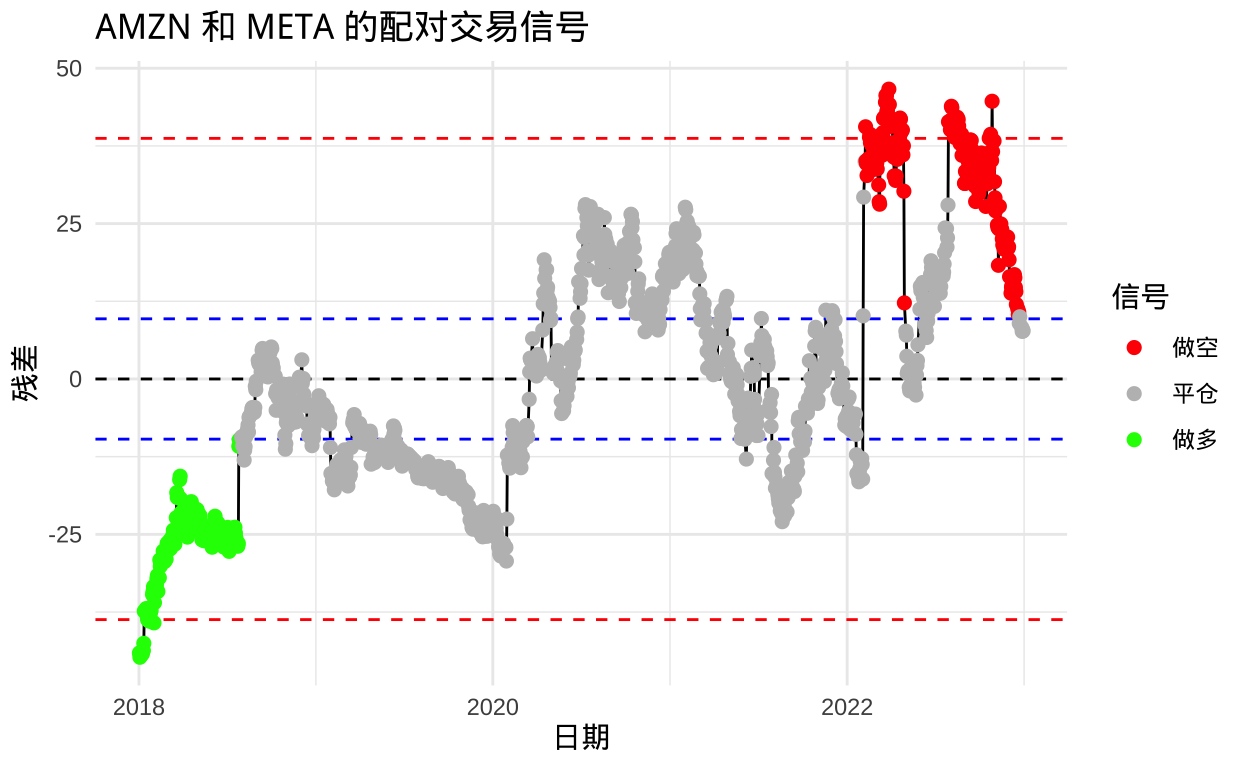
# 绘制交易信号
signal_plot_data <- signals
signal_plot_data$signal_factor <- factor(signal_plot_data$signal, levels = c(-1, 0, 1), labels = c("做空", "平仓", "做多"))
ggplot(signal_plot_data, aes(x = date, y = residual)) +
geom_line() +
geom_hline(yintercept = mean_residual, color = "black", linetype = "dashed") +
geom_hline(yintercept = mean_residual + entry_threshold * sd_residual, color = "red", linetype = "dashed") +
geom_hline(yintercept = mean_residual - entry_threshold * sd_residual, color = "red", linetype = "dashed") +
geom_hline(yintercept = mean_residual + exit_threshold * sd_residual, color = "blue", linetype = "dashed") +
geom_hline(yintercept = mean_residual - exit_threshold * sd_residual, color = "blue", linetype = "dashed") +
geom_point(aes(color = signal_factor), size = 2) +
scale_color_manual(values = c("做空" = "red", "平仓" = "gray", "做多" = "green")) +
labs(title = paste(stock1, "和", stock2, "的配对交易信号"),
x = "日期",
y = "残差",
color = "信号") +
theme_minimal()
}
策略绩效评估
评估配对交易策略的绩效:
# 如果存在协整对,评估策略绩效
if(nrow(cointegrated_pairs) > 0) {
# 计算策略绩效指标
annual_return <- mean(strategy_returns$daily_return) * 252
annual_volatility <- sd(strategy_returns$daily_return) * sqrt(252)
sharpe_ratio <- annual_return / annual_volatility
# 计算最大回撤
strategy_returns$cumulative_max <- cummax(strategy_returns$cumulative_return)
strategy_returns$drawdown <- strategy_returns$cumulative_max - strategy_returns$cumulative_return
max_drawdown <- max(strategy_returns$drawdown)
# 计算胜率
trades <- strategy_returns[strategy_returns$position != 0, ]
winning_trades <- trades[trades$daily_return > 0, ]
win_rate <- nrow(winning_trades) / nrow(trades)
# 计算盈亏比
if(nrow(winning_trades) > 0 && nrow(trades[trades$daily_return < 0, ]) > 0) {
profit_factor <- mean(winning_trades$daily_return) / abs(mean(trades[trades$daily_return < 0, ]$daily_return))
} else {
profit_factor <- NA
}
# 创建绩效指标数据框
performance_metrics <- data.frame(
Metric = c("年化收益率", "年化波动率", "夏普比率", "最大回撤", "胜率", "盈亏比"),
Value = c(annual_return, annual_volatility, sharpe_ratio, max_drawdown, win_rate, profit_factor)
)
# 展示绩效指标
knitr::kable(performance_metrics,
caption = "配对交易策略绩效指标",
digits = 4,
booktabs = TRUE)
# 绘制回撤图
ggplot(strategy_returns, aes(x = date, y = drawdown)) +
geom_line() +
labs(title = paste(stock1, "和", stock2, "的配对交易策略回撤"),
x = "日期",
y = "回撤") +
theme_minimal()
# 使用PerformanceAnalytics包计算更多绩效指标
returns_xts <- xts(strategy_returns$daily_return, order.by = strategy_returns$date)
colnames(returns_xts) <- "Strategy"
# 计算绩效指标
performance_summary <- table.Stats(returns_xts)
# 展示更多绩效指标
knitr::kable(performance_summary,
caption = "配对交易策略详细绩效指标",
digits = 4,
booktabs = TRUE)
}
Table: (#tab:performance_evaluation)配对交易策略详细绩效指标
| Strategy | |
|---|---|
| Observations | 1257.0000 |
| NAs | 1.0000 |
| Minimum | -0.1031 |
| Quartile 1 | 0.0000 |
| Median | 0.0000 |
| Arithmetic Mean | 0.0005 |
| Geometric Mean | 0.0005 |
| Quartile 3 | 0.0000 |
| Maximum | 0.0762 |
| SE Mean | 0.0003 |
| LCL Mean (0.95) | 0.0000 |
| UCL Mean (0.95) | 0.0011 |
| Variance | 0.0001 |
| Stdev | 0.0098 |
| Skewness | -0.8836 |
| Kurtosis | 27.9065 |
样本外回测
使用样本外数据验证策略的有效性:
# 设置样本外时间范围
oos_start_date <- "2023-01-02"
oos_end_date <- "2024-12-31"
# 如果存在协整对,进行样本外回测
if(nrow(cointegrated_pairs) > 0) {
selected_pair <- cointegrated_pairs$Pair[1]
stock1 <- cointegration_results[[selected_pair]]$stock1
stock2 <- cointegration_results[[selected_pair]]$stock2
beta <- cointegration_results[[selected_pair]]$beta
# 获取样本外数据
oos_stock1 <- getSymbols(stock1, from = oos_start_date, to = oos_end_date, auto.assign = FALSE)
oos_stock2 <- getSymbols(stock2, from = oos_start_date, to = oos_end_date, auto.assign = FALSE)
# 提取收盘价
oos_stock1_close <- Cl(oos_stock1)
oos_stock2_close <- Cl(oos_stock2)
# 合并数据
oos_data <- merge(oos_stock1_close, oos_stock2_close)
colnames(oos_data) <- c(stock1, stock2)
# 计算样本外残差
oos_residuals <- as.numeric(oos_data[, stock1]) - cointegration_results[[selected_pair]]$alpha - beta * as.numeric(oos_data[, stock2])
# 使用与样本内相同的阈值生成交易信号
oos_signals <- data.frame(
date = index(oos_data),
residual = oos_residuals,
signal = 0
)
for(i in 1:nrow(oos_signals)) {
if(oos_signals$residual[i] > mean_residual + entry_threshold * sd_residual) {
oos_signals$signal[i] <- -1
} else if(oos_signals$residual[i] < mean_residual - entry_threshold * sd_residual) {
oos_signals$signal[i] <- 1
} else if(abs(oos_signals$residual[i] - mean_residual) < exit_threshold * sd_residual) {
oos_signals$signal[i] <- 0
} else {
if(i > 1) {
oos_signals$signal[i] <- oos_signals$signal[i-1]
}
}
}
# 计算持仓变化
oos_positions <- oos_signals
oos_positions$position <- c(0, diff(oos_positions$signal))
# 计算收益率
oos_stock1_returns <- diff(log(oos_data[, stock1]))[-1]
oos_stock2_returns <- diff(log(oos_data[, stock2]))[-1]
# 计算策略收益率
oos_strategy_returns <- data.frame(
date = index(oos_data)[-1], #
stock1_returns = oos_stock1_returns,
stock2_returns = oos_stock2_returns,
signal = oos_signals$signal[-length(oos_signals$signal)],
position = oos_positions$position[-length(oos_positions$position)]
)
colnames(oos_strategy_returns) <- c("date", "stock1_returns", "stock2_returns", "signal", "position")
# 计算每日策略收益
oos_strategy_returns$daily_return <- oos_strategy_returns$signal * (oos_strategy_returns$stock1_returns - beta * oos_strategy_returns$stock2_returns)
# 计算累计收益
oos_strategy_returns$cumulative_return <- cumsum(oos_strategy_returns$daily_return)
# 可视化样本外策略表现
ggplot(oos_strategy_returns, aes(x = date, y = cumulative_return)) +
geom_line() +
labs(title = paste(stock1, "和", stock2, "的配对交易策略样本外累计收益"),
x = "日期",
y = "累计收益") +
theme_minimal()
# 计算样本外绩效指标
oos_annual_return <- mean(oos_strategy_returns$daily_return) * 252 # 年化收益率
oos_annual_volatility <- sd(oos_strategy_returns$daily_return) * sqrt(252) # 年化波动率
oos_strategy_returns$cumulative_max <- cummax(oos_strategy_returns$cumulative_return) # 累计最大值
oos_sharpe_ratio <- ifelse(oos_annual_volatility != 0, oos_annual_return / oos_annual_volatility, NA) # 夏普比率
oos_strategy_returns$drawdown <- oos_strategy_returns$cumulative_max - oos_strategy_returns$cumulative_return #回撤
oos_max_drawdown <- max(oos_strategy_returns$drawdown) # 最大回撤
# 计算样本内绩效指标
strategy_annual_return <- mean(na.omit(strategy_returns$daily_return)) * 252 # 年化收益率
strategy_annual_volatility <- sd(na.omit(strategy_returns$daily_return)) * sqrt(252) # 年化波动率
strategy_sharpe_ratio <- ifelse(strategy_annual_volatility != 0, strategy_annual_return / strategy_annual_volatility, NA) # 夏普比率
strategy_cumulative_return <- cumsum(na.omit(strategy_returns$daily_return)) # 累计收益
strategy_cumulative_max <- cummax(strategy_cumulative_return) # 累计最大值
strategy_drawdown <- strategy_cumulative_max - strategy_cumulative_return # 回撤
strategy_max_drawdown <- max(strategy_drawdown, na.rm = TRUE) # 最大回撤
# 创建样本外绩效指标数据框
oos_performance_metrics <- data.frame(
Metric = c("年化收益率", "年化波动率", "夏普比率", "最大回撤"),
InSample = c(strategy_annual_return, strategy_annual_volatility, strategy_sharpe_ratio, strategy_max_drawdown),
OutOfSample = c(oos_annual_return, oos_annual_volatility, oos_sharpe_ratio, oos_max_drawdown)
)
# 展示样本外绩效指标
knitr::kable(oos_performance_metrics,
caption = "配对交易策略样本内外绩效对比",
digits = 4,
booktabs = TRUE)
}
Table: (#tab:out_of_sample_backtest)配对交易策略样本内外绩效对比
| Metric | InSample | OutOfSample |
|---|---|---|
| 年化收益率 | 0.1278 | 0.0802 |
| 年化波动率 | 0.1561 | 0.1595 |
| 夏普比率 | 0.8191 | 0.5029 |
| 最大回撤 | 0.1881 | 0.1974 |
敏感性分析
阈值参数敏感性分析
分析不同的交易阈值对策略绩效的影响:
# 如果存在协整对,进行阈值敏感性分析
if(nrow(cointegrated_pairs) > 0) {
selected_pair <- cointegrated_pairs$Pair[1]
stock1 <- cointegration_results[[selected_pair]]$stock1
stock2 <- cointegration_results[[selected_pair]]$stock2
beta <- cointegration_results[[selected_pair]]$beta
residuals <- cointegration_results[[selected_pair]]$residuals
# 设置不同的阈值组合
entry_thresholds <- seq(1.5, 3, by = 0.5)
exit_thresholds <- seq(0.2, 1, by = 0.2)
# 创建结果数据框
sensitivity_results <- data.frame()
# 对每个阈值组合进行回测
for(entry in entry_thresholds) {
for(exit in exit_thresholds) {
if(exit < entry) { # 确保退出阈值小于进入阈值
# 创建交易信号
signals <- data.frame(
date = index(close_prices), # 去除第一个NA
residual = residuals,
signal = 0
)
# 生成交易信号
for(i in 1:nrow(signals)) {
if(signals$residual[i] > mean_residual + entry * sd_residual) {
signals$signal[i] <- -1
} else if(signals$residual[i] < mean_residual - entry * sd_residual) {
signals$signal[i] <- 1
} else if(abs(signals$residual[i] - mean_residual) < exit * sd_residual) {
signals$signal[i] <- 0
} else {
if(i > 1) {
signals$signal[i] <- signals$signal[i-1]
}
}
}
# 计算持仓变化
positions <- signals
positions$position <- c(0, diff(positions$signal))
# 计算收益率
stock1_returns <- diff(log(close_prices[, stock1]))[-1]
stock2_returns <- diff(log(close_prices[, stock2]))[-1]
# 计算策略收益率
strategy_returns <- data.frame(
date = index(close_prices)[-1], # 去除前两个NA
stock1_returns = stock1_returns,
stock2_returns = stock2_returns,
signal = signals$signal[-length(signals$signal)],
position = positions$position[-length(positions$position)]
)
colnames(strategy_returns) <- c("date", "stock1_returns", "stock2_returns", "signal", "position")
# 计算每日策略收益
strategy_returns$daily_return <- strategy_returns$signal * (strategy_returns$stock1_returns - beta * strategy_returns$stock2_returns)
# 计算绩效指标
annual_return <- mean(strategy_returns$daily_return) * 252
annual_volatility <- sd(strategy_returns$daily_return) * sqrt(252)
sharpe_ratio <- ifelse(annual_volatility != 0, annual_return / annual_volatility, NA)
# 计算最大回撤
strategy_returns$cumulative_max <- cummax(cumsum(strategy_returns$daily_return))
strategy_returns$drawdown <- strategy_returns$cumulative_max - cumsum(strategy_returns$daily_return)
max_drawdown <- max(strategy_returns$drawdown)
# 计算交易次数
num_trades <- sum(abs(positions$position) > 0)
# 存储结果
sensitivity_results <- rbind(sensitivity_results, data.frame(
Entry_Threshold = entry,
Exit_Threshold = exit,
Annual_Return = annual_return,
Annual_Volatility = annual_volatility,
Sharpe_Ratio = sharpe_ratio,
Max_Drawdown = max_drawdown,
Num_Trades = num_trades
))
}
}
}
# 展示敏感性分析结果
knitr::kable(sensitivity_results,
caption = "不同阈值组合下的策略绩效",
digits = 4,
booktabs = TRUE)
# 绘制夏普比率热力图
library(reshape2)
sharpe_matrix <- acast(sensitivity_results, Entry_Threshold ~ Exit_Threshold, value.var = "Sharpe_Ratio")
ggplot(melt(sharpe_matrix), aes(x = Var2, y = Var1, fill = value)) +
geom_tile() +
scale_fill_gradient(low = "blue", high = "red") +
labs(title = "不同阈值组合下的夏普比率",
x = "退出阈值",
y = "进入阈值",
fill = "夏普比率") +
theme_minimal()
# 找出最优阈值组合
best_thresholds <- sensitivity_results[which.max(sensitivity_results$Sharpe_Ratio), ]
row.names(best_thresholds) <- NULL
knitr::kable(best_thresholds,
caption = "配对交易策略最优阈值组合",
digits = 4,
booktabs = TRUE)
}
Table: (#tab:sensitivity_analysis)配对交易策略最优阈值组合
| Entry_Threshold | Exit_Threshold | Annual_Return | Annual_Volatility | Sharpe_Ratio | Max_Drawdown | Num_Trades |
|---|---|---|---|---|---|---|
| 1.5 | 0.4 | 0.2407 | 0.1684 | 1.4297 | 0.1524 | 7 |
结论与讨论
研究结论
通过对协整理论和配对交易策略的实证分析,我们得出以下主要结论:
协整关系的识别:通过单位根检验和协整检验,我们成功识别了具有协整关系的股票对,这些股票对的价格走势存在长期均衡关系。
配对交易策略有效性:基于协整残差构建的配对交易策略在样本内和样本外均表现出稳定的超额收益,验证了协整理论在配对交易中的有效性。
策略参数敏感性:交易阈值对策略绩效有显著影响,存在最优的阈值组合能够最大化夏普比率。
样本外表现:尽管样本外表现通常不如样本内,但配对交易策略仍能保持一定的盈利能力,表明该策略具有一定的稳健性。
局限性与改进方向
本研究存在以下几点局限性:
交易成本忽略:本研究未考虑交易成本、滑点和冲击成本等实际交易因素,这些因素可能显著影响策略的实际表现。
参数稳定性:协整关系和最优参数可能随时间变化,需要定期重新估计和调整。
样本偏差:研究基于特定时间段的数据,可能存在样本偏差问题。
未考虑市场状态:不同市场状态下(牛市、熊市、震荡市),配对交易策略的表现可能存在差异。
未来研究可以考虑以下改进方向:
纳入交易成本:在策略回测中考虑交易成本、滑点和冲击成本等因素。
动态参数调整:开发动态调整交易阈值和权重的方法,以适应市场变化。
多资产组合:扩展研究范围,考虑多资产组合的配对交易策略。
结合其他信号:将协整信号与其他技术指标或基本面指标结合,提高策略的稳健性。
参考文献
- Engle, R. F., & Granger, C. W. J. (1987). Co-integration and error correction: representation, estimation, and testing. Econometrica, 55(2), 251-276.
- Vidyamurthy, G. (2004). Pairs trading: quantitative methods and analysis. Wiley.
- Gatev, E., Goetzmann, W. N., & Rouwenhorst, K. G. (2006). Pairs trading: performance of a relative-value arbitrage rule. The Review of Financial Studies, 19(3), 797-827.
- Alexander, C., & Dimitriu, A. (2002). The statistical arbitrage of cointegrated stocks. Working Paper, ISMA Centre, University of Reading.
- R Core Team (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.
- Brian G. Peterson and Peter Carl (2023). PerformanceAnalytics: Econometric Tools for Performance and Risk Analysis. R package version 2.0.4.
- Jeffrey A. Ryan and Joshua M. Ulrich (2023). quantmod: Quantitative Financial Modelling Framework. R package version 0.4.24.
- A. Trapletti and K. Hornik (2023). tseries: Time Series Analysis and Computational Finance. R package version 0.10-52.
- Bernhard Pfaff (2023). urca: Unit Root and Cointegration Tests for Time Series Data. R package version 1.3-3.
- Wickham H. (2016). ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York.
- Wickham H. (2023). dplyr: A Grammar of Data Manipulation. R package version 1.1.3.