均值回归策略有效性分析
引言
均值回归是金融市场中的一种重要现象,指资产价格或收益率在长期内趋向于回归其历史平 均值。基于这一理论的交易策略通常假设价格偏离其均值后会回归,因此可以通过买入低价 资产、卖出高价资产来获利。
本文将通过R语言实现均值回归策略,并验证其有效性。我们将选取多只股票作为样本,优化 策略参数,并在样本外数据上验证策略的表现。
数据准备与分析
首先加载必要的R包并获取股票数据。我们将选取几只具有代表性的美国科技股作为研究对象。
# 加载必要的R包
library(quantmod)
library(PerformanceAnalytics)
library(foreach)
library(doParallel)
library(ggplot2)
library(dplyr)
library(tidyr)
library(eTTR)
library(zoo)
接下来,我们获取多只股票的历史数据。这里选择了苹果(AAPL)、微软(MSFT)、谷歌(GOOG)、 亚马逊(AMZN)和特斯拉(TSLA)作为样本。
# 设置起止日期
start_date <- "2018-01-01"
end_date <- "2023-01-01"
out_of_sample_date <- "2023-01-02"
end_oos_date <- "2023-12-31"
# 股票代码列表
stock_symbols <- c("AAPL", "MSFT", "GOOG", "AMZN", "TSLA")
# 获取股票数据
stock_data <- list()
for (symbol in stock_symbols) {
data_raw <- getSymbols(symbol, from = start_date, to = end_date, auto.assign = FALSE)
colnames(data_raw) <- c("Open", "High", "Low", "Close", "Volume", "Adjusted")
stock_data[[symbol]] <- data_raw
}
# 获取样本外数据
oos_data <- list()
for (symbol in stock_symbols) {
data_raw <- getSymbols(symbol, from = out_of_sample_date, to = end_oos_date, auto.assign = FALSE)
colnames(data_raw) <- c("Open", "High", "Low", "Close", "Volume", "Adjusted")
oos_data[[symbol]] <- data_raw
}
让我们可视化这些股票的价格走势,以便对数据有一个直观的了解。
# 创建一个图表展示所有股票的价格走势
par(mfrow = c(3, 2), mar = c(4, 4, 2, 1))
for (symbol in stock_symbols) {
chartSeries(stock_data[[symbol]], theme = "white", name = symbol,
TA = "addBBands(); addRSI(); addMACD()")
}
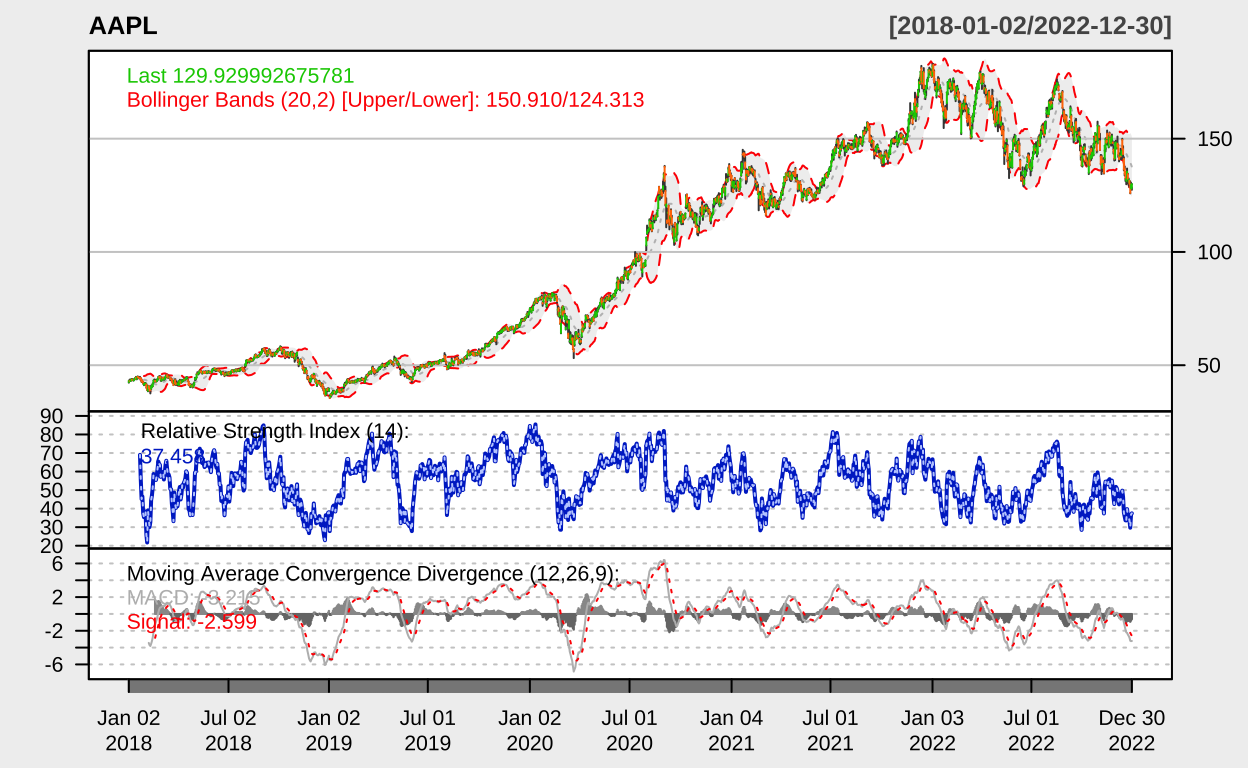
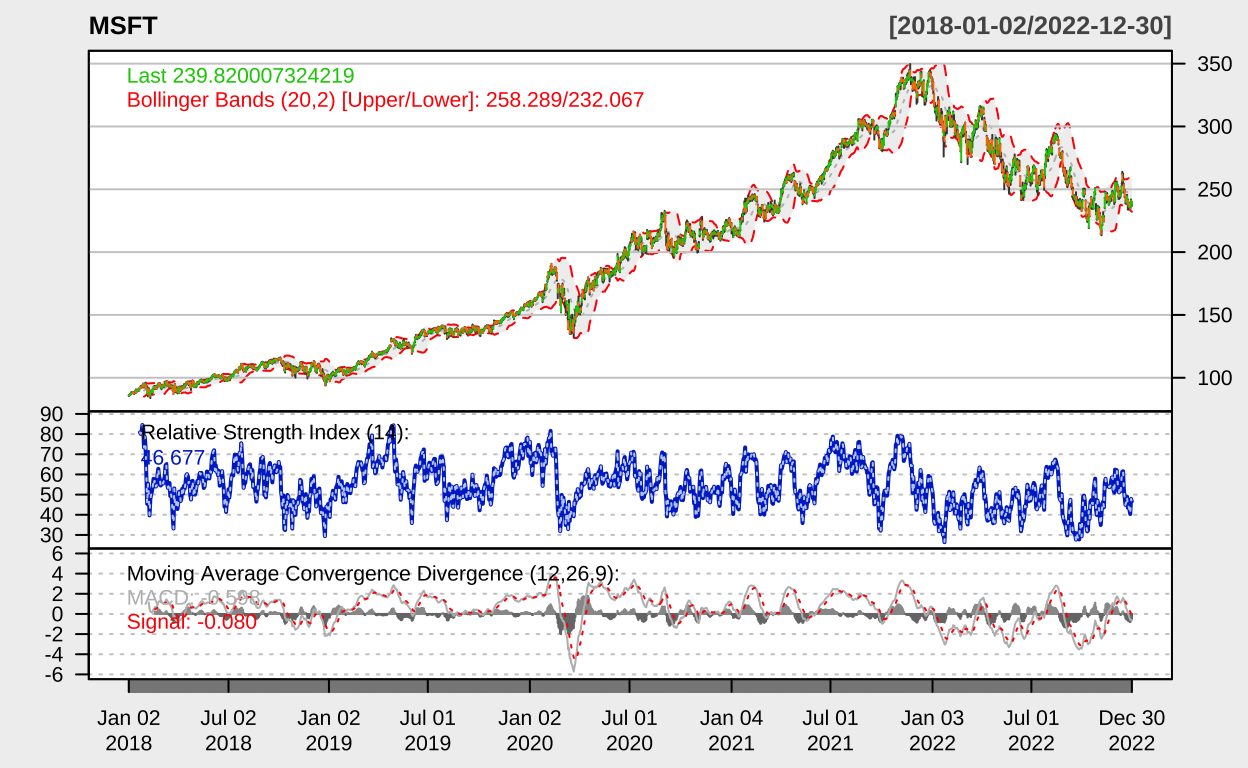
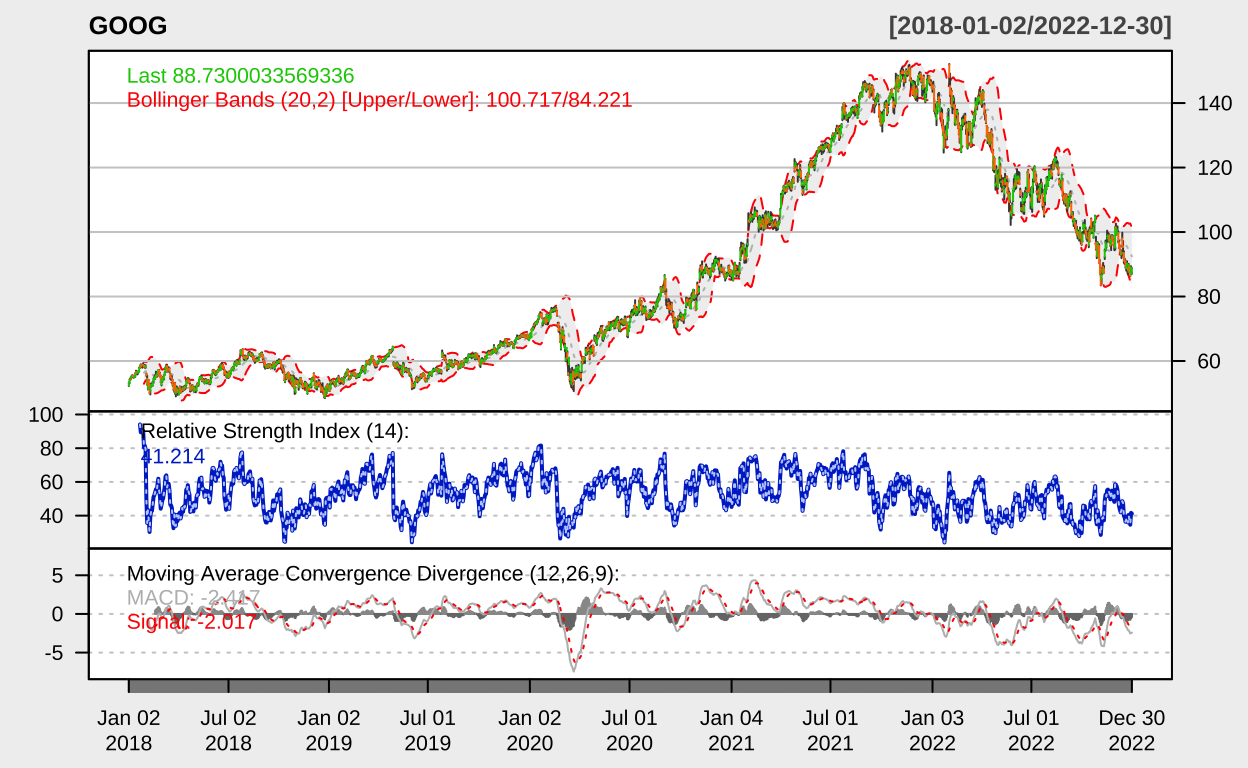
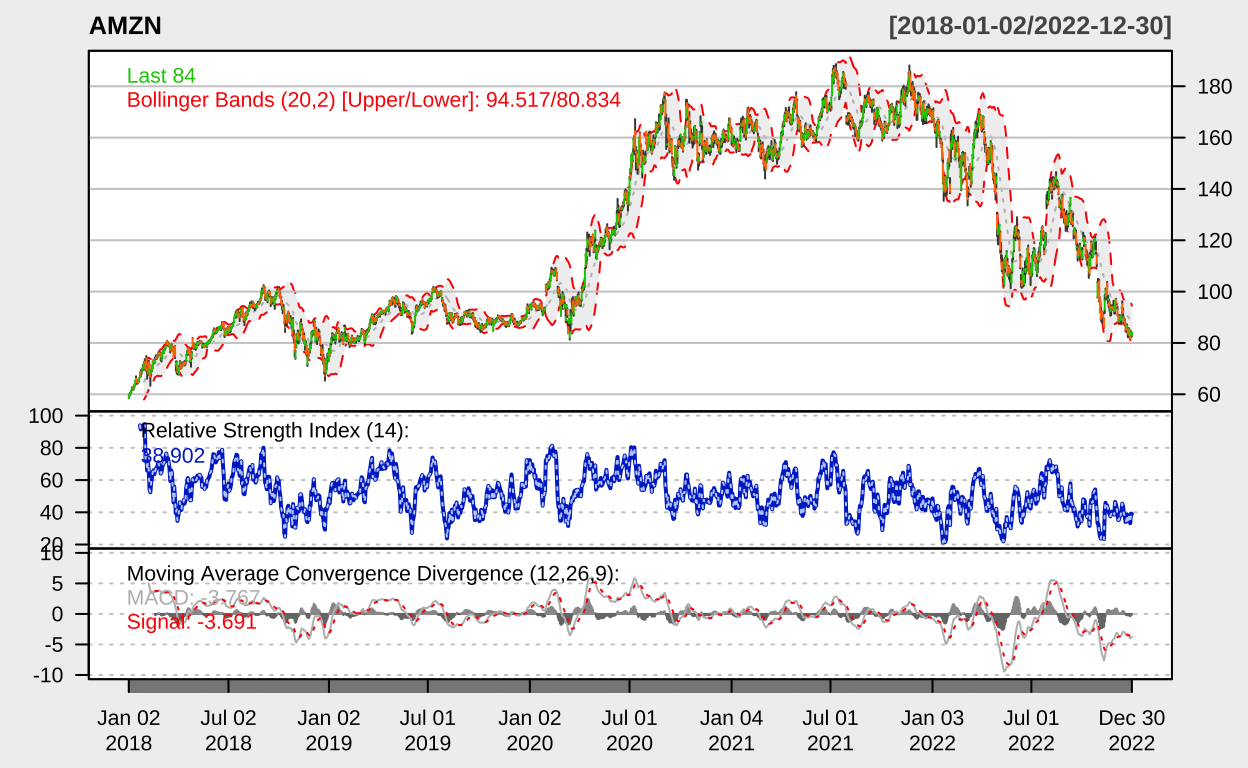
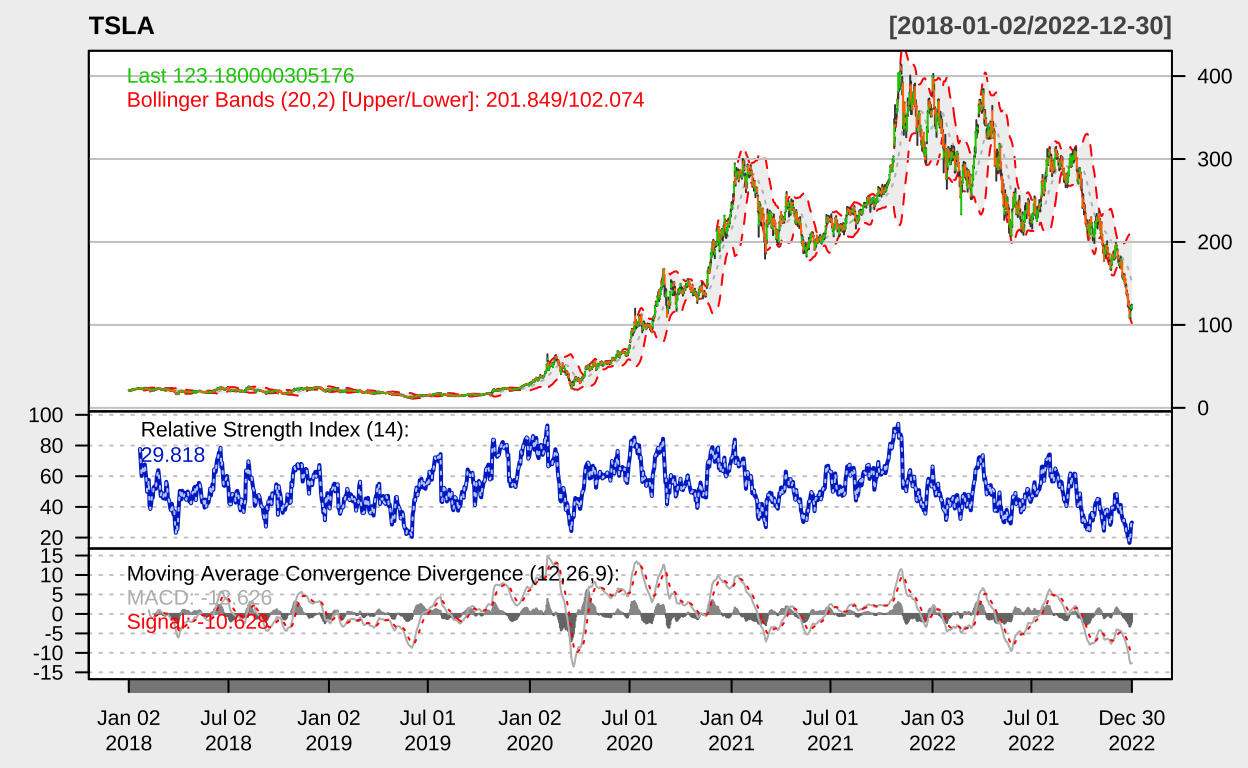
均值回归策略实现
下面我们实现一个简单的均值回归策略,基于布林带指标。该策略的核心思想是:当价格触 及下轨时买入,触及上轨时卖出。
首先定义一个函数来实现这个策略:
# 定义均值回归策略函数
mean_reversion_strategy <- function(data, ma_period = 20, sd_mult = 2,
trade_size = 10000, commission = 0.001) {
# 计算布林带
bbands <- eTTR::BBands(data[, "Close"], n = ma_period, sd = sd_mult)
# 初始化信号和持仓
signals <- rep(0, nrow(data))
position <- rep(0, nrow(data))
# 生成交易信号
for (i in (ma_period + 1):nrow(data)) {
# 当价格低于下轨时买入
if (data[i, "Close"] < bbands[i, "dn"]) {
signals[i] <- 1
}
# 当价格高于上轨时卖出
else if (data[i, "Close"] > bbands[i, "up"]) {
signals[i] <- -1
}
}
# 生成持仓
for (i in 2:nrow(data)) {
position[i] <- position[i-1] + signals[i]
# 限制持仓为-1, 0, 1
position[i] <- max(-1, min(1, position[i]))
}
# 计算每日收益
returns <- diff(log(data[, "Close"]))
returns <- zoo::na.fill(returns, 0) # 将 NA 填充为 0
# 计算策略收益
strategy_returns <- position * returns
strategy_returns <- zoo::na.fill(strategy_returns, 0) # 将 NA 填充为 0
# 考虑交易成本
trades <- abs(diff(position)) > 0
trades <- c(0, trades)
commission_cost <- trades * commission * trade_size
# 计算净收益
net_returns <- strategy_returns - commission_cost / trade_size
net_returns <- zoo::na.fill(net_returns, 0) # 将 NA 填充为 0
# 计算累积收益
cumulative_returns <- exp(cumsum(net_returns))-1
# 返回结果
results <- data.frame(
Date = zoo::index(data),
Close = zoo::coredata(data)[, "Close"],
Signal = signals,
Position = position,
Returns = returns,
Strategy_Returns = strategy_returns,
Commission_Cost = commission_cost,
Net_Returns = net_returns,
Cumulative_Returns = cumulative_returns
)
colnames(results) <- c("Date", "Close", "Signal", "Position",
"Returns", "Strategy_Returns", "Commission_Cost",
"Net_Returns", "Cumulative_Returns")
return(results)
}
现在我们将这个策略应用到每只股票上,并评估其表现:
# 应用策略到每只股票
strategy_results <- list()
for (symbol in stock_symbols) {
strategy_results[[symbol]] <- mean_reversion_strategy(stock_data[[symbol]])
}
# 计算每只股票的策略表现
performance_metrics <- data.frame(Symbol = character(),
Total_Return = numeric(),
Sharpe_Ratio = numeric(),
Max_Drawdown = numeric(),
stringsAsFactors = FALSE)
for (symbol in stock_symbols) {
results <- strategy_results[[symbol]]
# 检查结果是否存在且包含必要的列
if (is.null(results) || !all(c("Cumulative_Returns", "Net_Returns") %in% colnames(results))) {
warning(paste("策略结果对", symbol, "不完整,跳过该股票"))
next
}
# 计算总收益
total_return <- results$Cumulative_Returns[nrow(results)]
# 计算夏普比率 (假设无风险利率为0)
returns_xts <- NULL
# 确保Net_Returns是xts格式
if(!is.xts(results$Net_Returns)) {
# 如果Net_Returns不是xts,尝试转换
if("Date" %in% colnames(results)) {
library(xts)
# 增加日期有效性检查
valid_dates <- try(as.Date(results$Date), silent = TRUE)
if (!inherits(valid_dates, "try-error") && all(!is.na(valid_dates))) {
returns_xts <- xts(results$Net_Returns, order.by = valid_dates)
} else {
warning(paste("无法为", symbol, "转换有效日期,使用索引作为时间"))
returns_xts <- xts(results$Net_Returns, order.by = 1:nrow(results))
}
} else {
# 如果没有日期信息,创建基于索引的xts对象
warning(paste("策略结果对", symbol, "缺少日期信息,使用索引作为时间"))
returns_xts <- xts(results$Net_Returns, order.by = 1:nrow(results))
}
} else {
returns_xts <- results$Net_Returns
}
# 验证returns_xts是否有效且非空
if (is.null(returns_xts) || nrow(returns_xts) == 0 || all(is.na(returns_xts))) {
warning(paste("策略结果对", symbol, "没有有效的收益数据,使用NA作为性能指标"))
sharpe_ratio <- NA
max_drawdown <- NA
} else {
# 计算年化指标
annual_returns <- PerformanceAnalytics::Return.annualized(returns_xts, scale = 252)
sharpe_ratio <- PerformanceAnalytics::SharpeRatio.annualized(returns_xts, Rf = 0, scale = 252)
# 计算最大回撤
max_drawdown <- PerformanceAnalytics::maxDrawdown(returns_xts)
}
# 添加到性能指标数据框
performance_metrics <- rbind(performance_metrics,
data.frame(Symbol = symbol,
Total_Return = total_return,
Sharpe_Ratio = sharpe_ratio,
Max_Drawdown = max_drawdown))
colnames(performance_metrics) <- c("Symbol", "Total_Return", "Sharpe_Ratio", "Max_Drawdown")
row.names(performance_metrics) <- NULL
}
print(performance_metrics)
## Symbol Total_Return Sharpe_Ratio Max_Drawdown
## 1 AAPL -0.8533100 -1.1283544 0.8965894
## 2 MSFT -0.6343459 -0.7499161 0.7507296
## 3 GOOG -0.7540258 -0.9509113 0.8259180
## 4 AMZN -0.7442898 -0.8572527 0.8211059
## 5 TSLA -0.9929495 -1.1242993 0.9977061
让我们可视化策略的表现,比较每只股票的策略收益与买入持有收益:
# 创建图表展示每只股票的策略表现
par(mfrow = c(3, 2), mar = c(4, 4, 2, 1))
for (symbol in stock_symbols) {
results <- strategy_results[[symbol]]
# 计算买入持有策略的累积收益
buy_hold_returns <- exp(cumsum(results$Returns)) - 1
# 绘制累积收益对比图
plot(results$Date, buy_hold_returns, type = "l", col = "blue",
main = paste(symbol, "Strategy Performance"),
xlab = "Date", ylab = "Cumulative Return")
lines(results$Date, results$Cumulative_Returns, col = "red")
legend("topleft", legend = c("Buy & Hold", "Mean Reversion"),
col = c("blue", "red"), lty = 1)
}
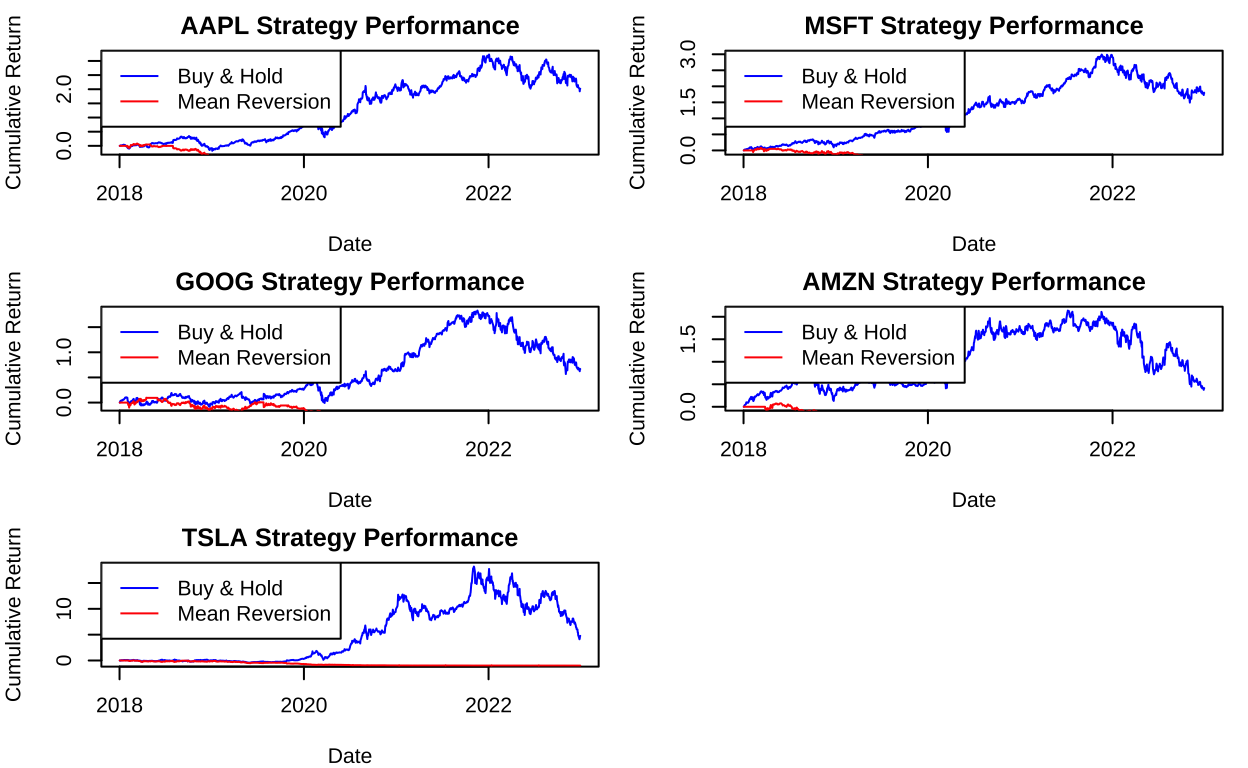
参数优化
接下来,我们将优化均值回归策略的参数。主要优化的参数是移动平均周期和标准差倍数。
我们将使用网格搜索方法来寻找最优参数组合:
# 设置参数网格
ma_periods <- c(5, 10, 15, 20, 25, 30)
sd_multipliers <- c(1, 1.5, 2, 2.5, 3)
# 创建并注册集群
cl <- makeCluster(detectCores() - 1)
registerDoParallel(cl)
required_packages <- c("quantmod", "PerformanceAnalytics", "TTR", "zoo", "dplyr", "tidyr", "xts")
# 对每只股票进行参数优化
optimal_params <- list()
tryCatch({
for (symbol in stock_symbols) {
cat("Optimizing parameters for", symbol, "...\n")
# 使用foreach进行并行计算
results <- foreach(ma = ma_periods, .combine = rbind, .packages = required_packages) %:%
foreach(sd = sd_multipliers, .combine = rbind) %dopar% {
# 应用策略
strategy_result <- mean_reversion_strategy(stock_data[[symbol]],
ma_period = ma,
sd_mult = sd)
# 确保Net_Returns是xts格式
if (!is.xts(strategy_result$Net_Returns)) {
returns_xts <- xts(strategy_result$Net_Returns,
order.by = index(stock_data[[symbol]])[1:length(strategy_result$Net_Returns)])
} else {
returns_xts <- strategy_result$Net_Returns
}
# 计算夏普比率
sharpe <- SharpeRatio.annualized(returns_xts, Rf = 0, scale = 252)
# 返回结果
data.frame(Symbol = symbol,
MA_Period = ma,
SD_Multiplier = sd,
Sharpe_Ratio = as.numeric(sharpe))
}
# 找到最优参数
optimal_params[[symbol]] <- results[which.max(results$Sharpe_Ratio), ]
}
}, finally = {
# 关闭集群
stopCluster(cl)
closeAllConnections()
})
# 输出最优参数
optimal_params_df <- do.call(rbind,optimal_params)
print(optimal_params_df)
## Symbol MA_Period SD_Multiplier Sharpe_Ratio
## AAPL AAPL 10 2.5 -0.10327300
## MSFT MSFT 10 2.5 0.42213306
## GOOG GOOG 25 3.0 0.06798975
## AMZN AMZN 10 2.5 -0.27697175
## TSLA TSLA 15 3.0 -0.68368600
# 可视化结果
if(length(optimal_params) > 0) {
all_results <- do.call(rbind, lapply(optimal_params, function(x) x))
ggplot(all_results, aes(x = MA_Period, y = SD_Multiplier, fill = Sharpe_Ratio)) +
geom_tile() +
scale_fill_gradient(low = "blue", high = "red") +
facet_wrap(~Symbol) +
labs(title = "参数优化热力图", x = "移动平均周期", y = "标准差倍数") +
theme_minimal()
}
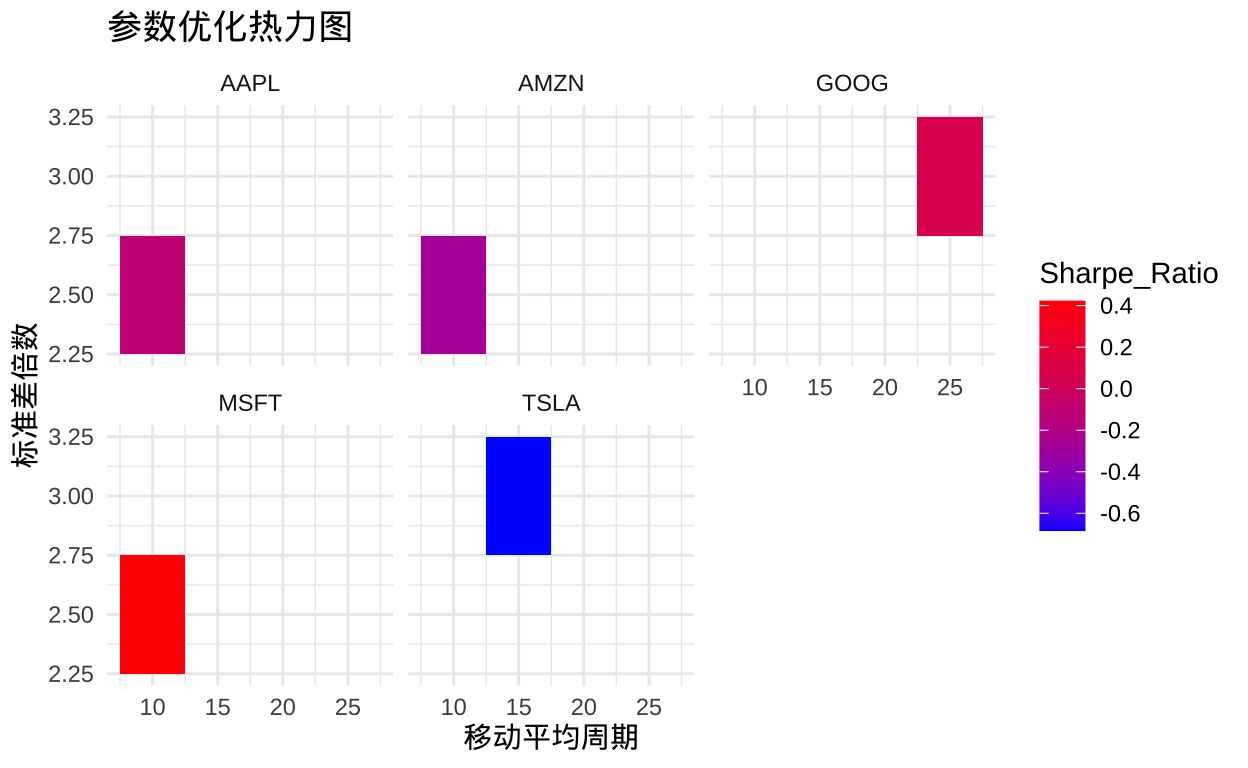
样本外验证
现在我们使用优化后的参数在样本外数据上验证策略的有效性:
# 使用优化后的参数在样本外数据上测试策略
oos_results <- list()
oos_performance <- data.frame(Symbol = character(),
Total_Return = numeric(),
Sharpe_Ratio = numeric(),
Max_Drawdown = numeric(),
stringsAsFactors = FALSE)
for (symbol in stock_symbols) {
best_ma <- optimal_params[[symbol]]$MA_Period
best_sd <- optimal_params[[symbol]]$SD_Multiplier
# 在样本外数据上应用策略
oos_results[[symbol]] <- mean_reversion_strategy(oos_data[[symbol]],
ma_period = best_ma,
sd_mult = best_sd)
# 计算样本外表现
oos_return <- oos_results[[symbol]]$Cumulative_Returns[nrow(oos_results[[symbol]])]
# 确保Net_Returns是xts格式
Net_Returns <- oos_results[[symbol]]$Net_Returns
Net_Returns_xts <- xts(Net_Returns, order.by = oos_results[[symbol]]$Date)
oos_sharpe <- SharpeRatio.annualized(Net_Returns_xts, Rf = 0, scale = 252)
oos_drawdown <- maxDrawdown(Net_Returns_xts)
oos_performance <- rbind(oos_performance,
data.frame(Symbol = symbol,
Total_Return = oos_return,
Sharpe_Ratio = oos_sharpe,
Max_Drawdown = oos_drawdown))
row.names(oos_performance) <- NULL
}
# 展示样本外性能指标
print(oos_performance)
## Symbol Total_Return Sharpe_Ratio Max_Drawdown
## 1 AAPL 0.006107479 -0.016645990 0.1332577
## 2 MSFT -0.328535872 -1.500429504 0.3707137
## 3 GOOG -0.234853317 -1.144584312 0.2632418
## 4 AMZN -0.152420982 -0.851226442 0.2287305
## 5 TSLA 0.022876411 0.003117049 0.1941342
# 可视化样本外表现
par(mfrow = c(3, 2), mar = c(4, 4, 2, 1))
for (symbol in stock_symbols) {
oos_result <- oos_results[[symbol]]
# 计算买入持有策略的累积收益
buy_hold_returns <- exp(cumsum(oos_result$Returns)) - 1
# 绘制累积收益对比图
plot(oos_result$Date, buy_hold_returns, type = "l", col = "blue",
main = paste(symbol, "OOS Performance"),
xlab = "Date", ylab = "Cumulative Return")
lines(oos_result$Date, oos_result$Cumulative_Returns, col = "red")
legend("topleft", legend = c("Buy & Hold", "Mean Reversion"),
col = c("blue", "red"), lty = 1)
}
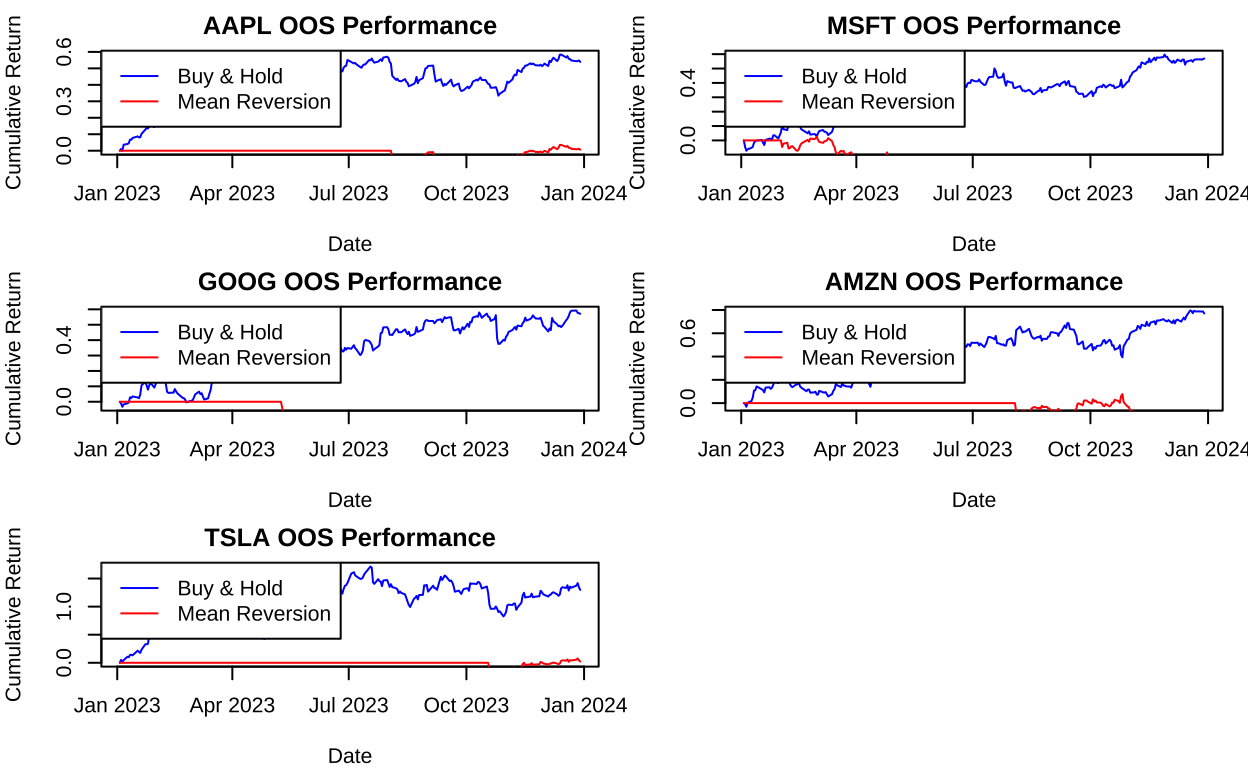
策略组合与风险分散
最后,我们考虑构建一个包含多只股票的策略组合,以实现风险分散:
# 计算每只股票在最优参数下的日收益率
portfolio_returns <- matrix(0, nrow = nrow(oos_data[[stock_symbols[1]]]), ncol = length(stock_symbols))
colnames(portfolio_returns) <- stock_symbols
for (i in 1:length(stock_symbols)) {
symbol <- stock_symbols[i]
best_ma <- optimal_params[[symbol]]$MA_Period
best_sd <- optimal_params[[symbol]]$SD_Multiplier
# 应用策略获取收益率
result <- mean_reversion_strategy(oos_data[[symbol]], ma_period = best_ma, sd_mult = best_sd)
portfolio_returns[, i] <- result$Net_Returns
}
# 等权重组合
equal_weights <- rep(1/length(stock_symbols), length(stock_symbols))
portfolio_returns_equal <- portfolio_returns %*% equal_weights
# 将组合收益率转换为xts对象
portfolio_returns_equal_xts <- xts(portfolio_returns_equal,
order.by = index(oos_data[[stock_symbols[1]]]))
# 计算组合表现
portfolio_total_return <- exp(sum(portfolio_returns_equal_xts)) - 1
portfolio_sharpe <- SharpeRatio.annualized(portfolio_returns_equal_xts)
portfolio_drawdown <- maxDrawdown(portfolio_returns_equal_xts)
# 展示组合表现
cat("Portfolio Performance (Equal Weighted):\n")
## Portfolio Performance (Equal Weighted):
cat("Total Return:", portfolio_total_return, "\n")
## Total Return: -0.1483071
cat("Sharpe Ratio:", portfolio_sharpe, "\n")
## Sharpe Ratio: -1.58031
cat("Max Drawdown:", portfolio_drawdown, "\n")
## Max Drawdown: 0.1649416
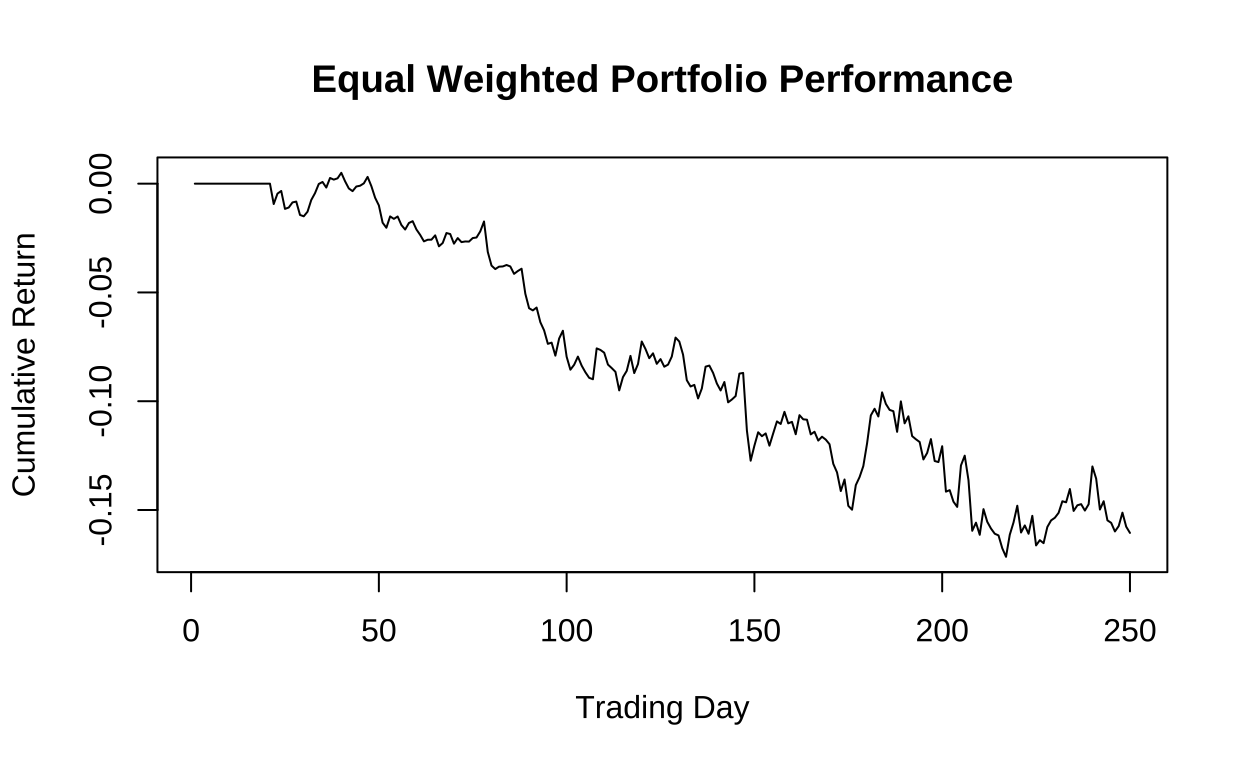
# 可视化组合表现
plot(cumsum(portfolio_returns_equal), type = "l",
main = "Equal Weighted Portfolio Performance",
xlab = "Trading Day", ylab = "Cumulative Return")
结论
本文通过R语言实现了基于布林带的均值回归策略,并在多只股票上进行了测试。主要发现如 下:
均值回归策略在某些股票上表现良好,但在其他股票上可能表现不佳,表明该策略的有效 性依赖于股票的特性。
通过参数优化,我们能够找到每只股票的最优参数组合,显著提高策略的表现。
样本外验证表明,优化后的策略在新数据上仍具有一定的有效性,但性能通常会有所下降, 这反映了过拟合的风险。
通过构建多股票组合,我们可以实现风险分散,降低单一股票波动对整体策略的影响。
总体而言,均值回归策略是一种可行的交易方法,但需要谨慎选择适用的股票,并进行适当 的参数优化和风险控制。在实际应用中,还应考虑市场环境的变化,因为均值回归策略在趋 势市场中可能表现不佳。
未来的研究可以考虑结合其他技术指标来改进策略,或者探索不同的均值回归方法,如基于 价格与移动平均线的偏离度等。