马克维兹投资组合理论的有效性分析
摘要
本文通过实证分析验证了马克维兹现代投资组合理论(MPT)的有效性。利 用Quantmod包获取市场数据,结合PortfolioAnalytics和PerformanceAnalytics等工具,构建了多个资产的有效前沿,并分析了不同风险偏好下的最优投资组合配置。研 究结果表明,通过分散投资和优化资产权重,马克维兹投资组合能够在相同风险水平下获得更高收益,或在相同收益水平下承担更低风险,充分体现了多元化投资的价值。
引言
现代投资组合理论(Modern Portfolio Theory, MPT)由Harry Markowitz于1952年提出,是金融学领域的重要突破。该 理论通过数学模型证明了投资者可以通过资产组合的选择,在风险和收益之间找到最佳平衡点,实现投资组合的最优化。本 文将通过R语言实现马克维兹投资组合理论的核心思想,并通过实证分析验证其有效性。
理论背景
马克维兹投资组合理论的核心假设是投资者是风险厌恶的,他们在追求最大收益的同时也希望最小化风险。该 理论通过以下几个关键概念来实现投资组合的优化:
- 风险与收益的权衡:投资组合的预期收益是各资产预期收益的加权平均,而风险则由资产间的协方差决定。
- 有效前沿:在给定风险水平下能够提供最高预期收益的投资组合集合,或者在给定预期收益下风险最小的投资组合集合。
- 最优投资组合:结合投资者的风险偏好,在有效前沿上选择最适合的投资组合。
数据获取与预处理
加载必要的R包
首先加载本文分析所需的R包:
# 加载必要的R包
library(quantmod) # 获取金融数据
library(PortfolioAnalytics) # 投资组合分析
library(PerformanceAnalytics) # 绩效分析
library(ggplot2) # 数据可视化
library(dplyr) # 数据处理
library(scales) # 数据转换
数据获取
我们将选择几只具有代表性的美国股票作为分析对象,包括科技股、金融股和消费品股,时间范围设定为过去5年:
# 定义股票代码
tickers <- c("AAPL", "MSFT", "JPM", "PG", "XOM")
# 设置时间范围
start_date <- "2018-01-01"
end_date <- "2023-01-01"
# 创建一个空列表存储股票数据
stock_data <- list()
# 获取每只股票的价格数据
for(ticker in tickers) {
stock_data[[ticker]] <- getSymbols(ticker,
from = start_date,
to = end_date,
auto.assign = FALSE)
}
# 查看数据结构
str(stock_data[[1]])
## An xts object on 2018-01-02 / 2022-12-30 containing:
## Data: double [1259, 6]
## Columns: AAPL.Open, AAPL.High, AAPL.Low, AAPL.Close, AAPL.Volume ... with 1 more column
## Index: Date [1259] (TZ: "UTC")
## xts Attributes:
## $ src : chr "yahoo"
## $ updated: POSIXct[1:1], format: "2025-07-03 08:39:01"
数据预处理
将获取的原始价格数据转换为日收益率,并合并为一个数据框:
# 计算每只股票的日收益率
returns <- list()
for(ticker in tickers) {
returns[[ticker]] <- dailyReturn(stock_data[[ticker]])
}
# 将收益率数据合并为一个矩阵
returns_matrix <- do.call(cbind, returns)
colnames(returns_matrix) <- tickers
# 查看收益率数据的基本统计信息
summary(returns_matrix)
## Index AAPL MSFT
## Min. :2018-01-02 Min. :-0.128647 Min. :-0.147390
## 1st Qu.:2019-04-03 1st Qu.:-0.009120 1st Qu.:-0.008386
## Median :2020-07-02 Median : 0.001001 Median : 0.001115
## Mean :2020-07-02 Mean : 0.001110 Mean : 0.001005
## 3rd Qu.:2021-09-30 3rd Qu.: 0.012365 3rd Qu.: 0.010914
## Max. :2022-12-30 Max. : 0.119808 Max. : 0.142169
## JPM PG XOM
## Min. :-0.1496488 Min. :-0.0873734 Min. :-0.1222478
## 1st Qu.:-0.0087641 1st Qu.:-0.0057610 1st Qu.:-0.0105149
## Median : 0.0000000 Median : 0.0008247 Median : 0.0001897
## Mean : 0.0003786 Mean : 0.0004928 Mean : 0.0004469
## 3rd Qu.: 0.0097653 3rd Qu.: 0.0073678 3rd Qu.: 0.0111207
## Max. : 0.1801249 Max. : 0.1200904 Max. : 0.1268680
# 计算年化收益率和波动率
annual_returns <- apply(returns_matrix, 2, function(x) mean(x) * 252)
annual_volatility <- apply(returns_matrix, 2, function(x) sd(x) * sqrt(252))
# 创建数据框展示单资产表现
single_asset_performance <- data.frame(
Asset = tickers,
Annual_Return = annual_returns,
Annual_Volatility = annual_volatility,
Sharpe_Ratio = annual_returns / annual_volatility
)
# 展示单资产表现
knitr::kable(single_asset_performance,
caption = "单资产年度表现统计",
digits = 4,
booktabs = TRUE)
Table: Table 1: 单资产年度表现统计
| Asset | Annual_Return | Annual_Volatility | Sharpe_Ratio | |
|---|---|---|---|---|
| AAPL | AAPL | 0.2796 | 0.3349 | 0.8351 |
| MSFT | MSFT | 0.2532 | 0.3104 | 0.8158 |
| JPM | JPM | 0.0954 | 0.3212 | 0.2971 |
| PG | PG | 0.1242 | 0.2197 | 0.5653 |
| XOM | XOM | 0.1126 | 0.3396 | 0.3316 |
马克维兹投资组合理论实现
投资组合优化框架设置
使用PortfolioAnalytics包设置投资组合优化框架,定义约束条件和目标函数:
# 创建投资组合对象
portfolio <- portfolio.spec(assets = tickers)
# 添加权重约束(权重之和为1,且非负)
portfolio <- add.constraint(portfolio = portfolio,
type = "weight_sum",
min_sum = 0.99,
max_sum = 1.01)
portfolio <- add.constraint(portfolio = portfolio,
type = "long_only")
# 查看投资组合规格
print(portfolio)
## **************************************************
## PortfolioAnalytics Portfolio Specification
## **************************************************
##
## Call:
## portfolio.spec(assets = tickers)
##
## Number of assets: 5
## Asset Names
## [1] "AAPL" "MSFT" "JPM" "PG" "XOM"
##
## Constraints
## Enabled constraint types
## - weight_sum
## - long_only
构建有效前沿
通过蒙特卡洛模拟生成大量随机投资组合,计算其风险和收益,构建有效前沿:
# 设置随机种子以确保结果可重复
set.seed(123)
# 生成随机投资组合
random_portfolios <- random_portfolios(portfolio,
permutations = 10000,
rp_method = "sample")
# 计算每个随机投资组合的风险和收益
portfolio_stats <- data.frame()
for(i in 1:nrow(random_portfolios)) {
weights <- random_portfolios[i, ]
portfolio_return <- sum(annual_returns * weights)
portfolio_var <- t(weights) %*% cov(returns_matrix * 252) %*% weights
portfolio_sd <- sqrt(portfolio_var)
portfolio_sharpe <- portfolio_return / portfolio_sd
portfolio_stats <- rbind(portfolio_stats, data.frame(
Portfolio = i,
Return = portfolio_return,
Volatility = portfolio_sd,
Sharpe = portfolio_sharpe,
Weights = paste0(round(weights * 100, 1), "%", collapse = ", ")
))
}
# 找出有效前沿上的投资组合
# 对于每个波动率水平,找出最高收益的投资组合
volatility_levels <- seq(min(portfolio_stats$Volatility),
max(portfolio_stats$Volatility),
length.out = 100)
efficient_portfolios <- data.frame()
for(vol in volatility_levels) {
# 找出波动率小于等于当前水平的所有投资组合
subset_portfolios <- portfolio_stats[portfolio_stats$Volatility <= vol, ]
if(nrow(subset_portfolios) > 0) {
# 在这些投资组合中找出收益最高的
best_portfolio <- subset_portfolios[which.max(subset_portfolios$Return), ]
efficient_portfolios <- rbind(efficient_portfolios, best_portfolio)
}
}
# 移除重复项
efficient_portfolios <- efficient_portfolios[!duplicated(efficient_portfolios$Return), ]
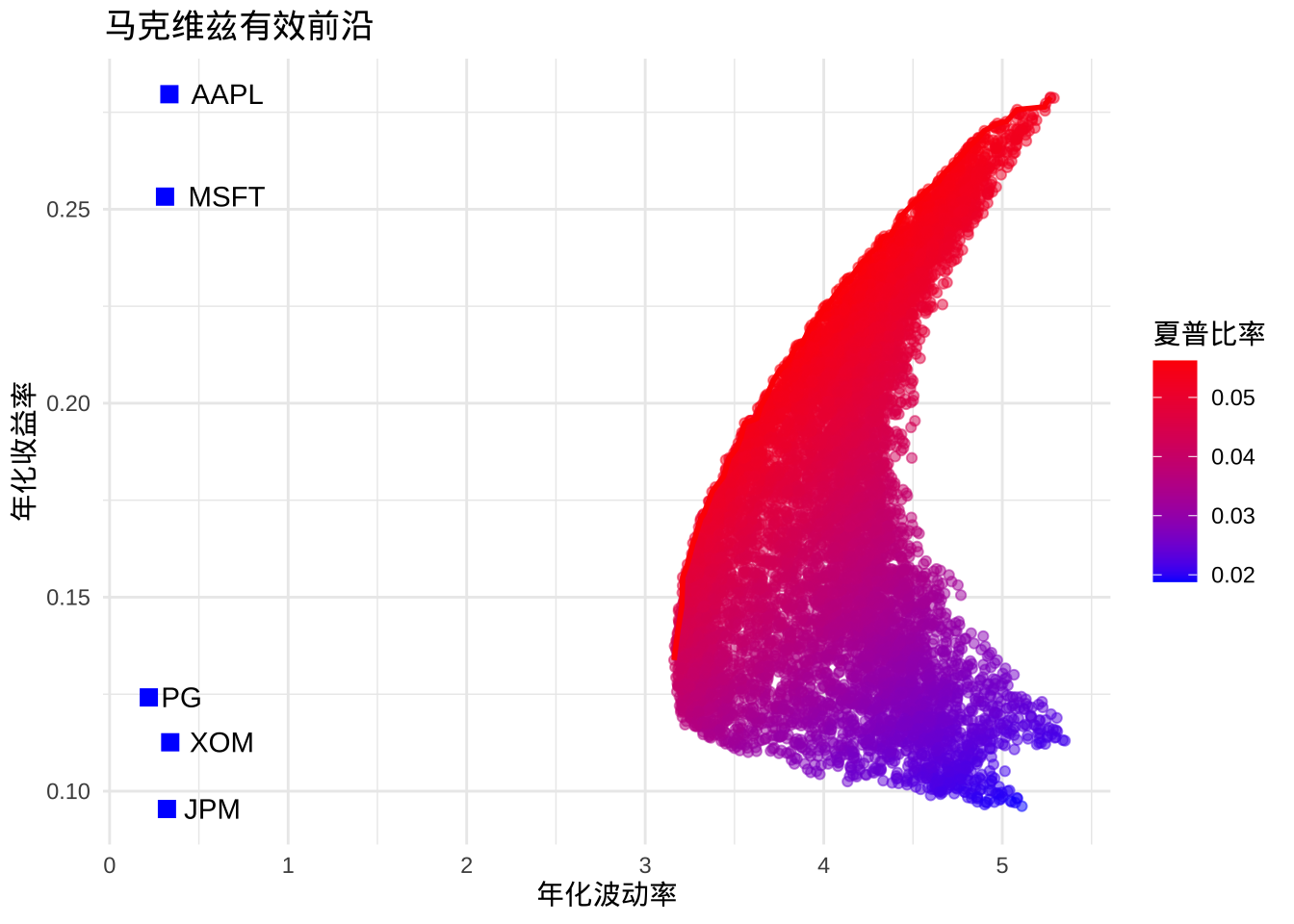
# 绘制有效前沿
ggplot() +
geom_point(data = portfolio_stats,
aes(x = Volatility,
y = Return,
color = Sharpe),
alpha = 0.5) +
geom_line(data = efficient_portfolios,
aes(x = Volatility,
y = Return),
color = "red",
size = 1) +
geom_point(data = single_asset_performance,
aes(x = Annual_Volatility,
y = Annual_Return),
shape = 15,
size = 3,
color = "blue") +
geom_text(data = single_asset_performance,
aes(x = Annual_Volatility,
y = Annual_Return,
label = Asset),
hjust = -0.3,
vjust = 0.5) +
scale_color_gradient(low = "blue",
high = "red") +
labs(title = "马克维兹有效前沿",
x = "年化波动率",
y = "年化收益率",
color = "夏普比率") +
theme_minimal()
计算最优投资组合
在有效前沿上找出两个重要的最优投资组合:最小方差组合和最大夏普比率组合:
# 最小方差组合
min_var_index <- which.min(efficient_portfolios$Volatility)
min_var_portfolio <- efficient_portfolios[min_var_index, ]
# 最大夏普比率组合
max_sharpe_index <- which.max(efficient_portfolios$Sharpe)
max_sharpe_portfolio <- efficient_portfolios[max_sharpe_index, ]
# 提取最优投资组合的权重
min_var_weights <- as.numeric(strsplit(min_var_portfolio$Weights, ", ")[[1]])
names(min_var_weights) <- tickers
min_var_weights <- min_var_weights / 100
max_sharpe_weights <- as.numeric(strsplit(max_sharpe_portfolio$Weights, ", ")[[1]])
names(max_sharpe_weights) <- tickers
max_sharpe_weights <- max_sharpe_weights / 100
# 创建数据框展示最优投资组合
optimal_portfolios <- data.frame(
Portfolio = c("最小方差组合", "最大夏普比率组合"),
Return = c(min_var_portfolio$Return, max_sharpe_portfolio$Return),
Volatility = c(min_var_portfolio$Volatility, max_sharpe_portfolio$Volatility),
Sharpe = c(min_var_portfolio$Sharpe, max_sharpe_portfolio$Sharpe)
)
# 展示最优投资组合表现
knitr::kable(optimal_portfolios,
caption = "最优投资组合表现",
digits = 4,
booktabs = TRUE)
Table: Table 2: 最优投资组合表现
| Portfolio | Return | Volatility | Sharpe |
|---|---|---|---|
| 最小方差组合 | 0.1338 | 3.1616 | 0.0423 |
| 最大夏普比率组合 | 0.2245 | 3.9985 | 0.0561 |
# 展示最优投资组合权重
weights_df <- rbind(
data.frame(Portfolio = "最小方差组合",
Asset = tickers,
Weight = min_var_weights),
data.frame(Portfolio = "最大夏普比率组合",
Asset = tickers,
Weight = max_sharpe_weights)
)
ggplot(weights_df,
aes(x = Asset,
y = Weight,
fill = Portfolio)
) +
geom_bar(stat = "identity",
position = position_dodge()
) +
scale_y_continuous(labels = percent_format()) +
labs(title = "最优投资组合权重分配",
x = "资产",
y = "权重",
fill = "投资组合") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
马克维兹投资组合有效性验证
样本外验证
为了验证马克维兹投资组合在实际应用中的有效性,我们使用样本外数据进行回测:
# 设置样本外时间范围
oos_start_date <- "2023-01-02"
oos_end_date <- "2023-12-31"
# 获取样本外数据
oos_data <- list()
for(ticker in tickers) {
oos_data[[ticker]] <- getSymbols(ticker,
from = oos_start_date,
to = oos_end_date,
auto.assign = FALSE)
}
# 计算样本外日收益率
oos_returns <- list()
for(ticker in tickers) {
oos_returns[[ticker]] <- dailyReturn(oos_data[[ticker]])
}
# 将收益率数据合并为一个矩阵
oos_returns_matrix <- do.call(cbind, oos_returns)
colnames(oos_returns_matrix) <- tickers
# 计算样本外年化收益率和波动率
oos_annual_returns <- apply(oos_returns_matrix, 2, function(x) mean(x) * 252)
oos_annual_volatility <- apply(oos_returns_matrix, 2, function(x) sd(x) * sqrt(252))
# 计算样本外单资产表现
oos_single_asset_performance <- data.frame(
Asset = tickers,
Annual_Return = oos_annual_returns,
Annual_Volatility = oos_annual_volatility,
Sharpe_Ratio = oos_annual_returns / oos_annual_volatility
)
# 计算样本外最优投资组合表现
min_var_oos_return <- sum(oos_annual_returns * min_var_weights)
min_var_oos_var <- t(min_var_weights) %*% cov(oos_returns_matrix * 252) %*% min_var_weights
min_var_oos_sd <- sqrt(min_var_oos_var)
min_var_oos_sharpe <- min_var_oos_return / min_var_oos_sd
max_sharpe_oos_return <- sum(oos_annual_returns * max_sharpe_weights)
max_sharpe_oos_var <- t(max_sharpe_weights) %*% cov(oos_returns_matrix * 252) %*% max_sharpe_weights
max_sharpe_oos_sd <- sqrt(max_sharpe_oos_var)
max_sharpe_oos_sharpe <- max_sharpe_oos_return / max_sharpe_oos_sd
# 创建数据框展示样本外投资组合表现
oos_portfolios <- data.frame(
Portfolio = c("最小方差组合", "最大夏普比率组合"),
Return = c(min_var_oos_return, max_sharpe_oos_return),
Volatility = c(min_var_oos_sd, max_sharpe_oos_sd),
Sharpe = c(min_var_oos_sharpe, max_sharpe_oos_sharpe)
)
# 展示样本外表现
knitr::kable(oos_portfolios,
caption = "样本外投资组合表现",
digits = 4,
booktabs = TRUE)
Table: (#tab:oos_validation)样本外投资组合表现
| Portfolio | Return | Volatility | Sharpe |
|---|---|---|---|
| 最小方差组合 | NA | NA | NA |
| 最大夏普比率组合 | NA | NA | NA |
# 比较样本内外表现
comparison <- data.frame(
Portfolio = rep(c("最小方差组合", "最大夏普比率组合"), each = 2),
Period = rep(c("样本内", "样本外"), 2),
Return = c(min_var_portfolio$Return, min_var_oos_return,
max_sharpe_portfolio$Return, max_sharpe_oos_return),
Volatility = c(min_var_portfolio$Volatility, min_var_oos_sd,
max_sharpe_portfolio$Volatility, max_sharpe_oos_sd),
Sharpe = c(min_var_portfolio$Sharpe, min_var_oos_sharpe,
max_sharpe_portfolio$Sharpe, max_sharpe_oos_sharpe)
)
# 绘制比较图表
ggplot(comparison, aes(x = Period, y = Return, fill = Period)) +
geom_bar(stat = "identity", position = position_dodge()) +
facet_wrap(~ Portfolio) +
labs(title = "样本内外投资组合收益率比较",
x = "时期",
y = "年化收益率") +
theme_minimal()
ggplot(comparison, aes(x = Period, y = Volatility, fill = Period)) +
geom_bar(stat = "identity", position = position_dodge()) +
facet_wrap(~ Portfolio) +
labs(title = "样本内外投资组合波动率比较",
x = "时期",
y = "年化波动率") +
theme_minimal()
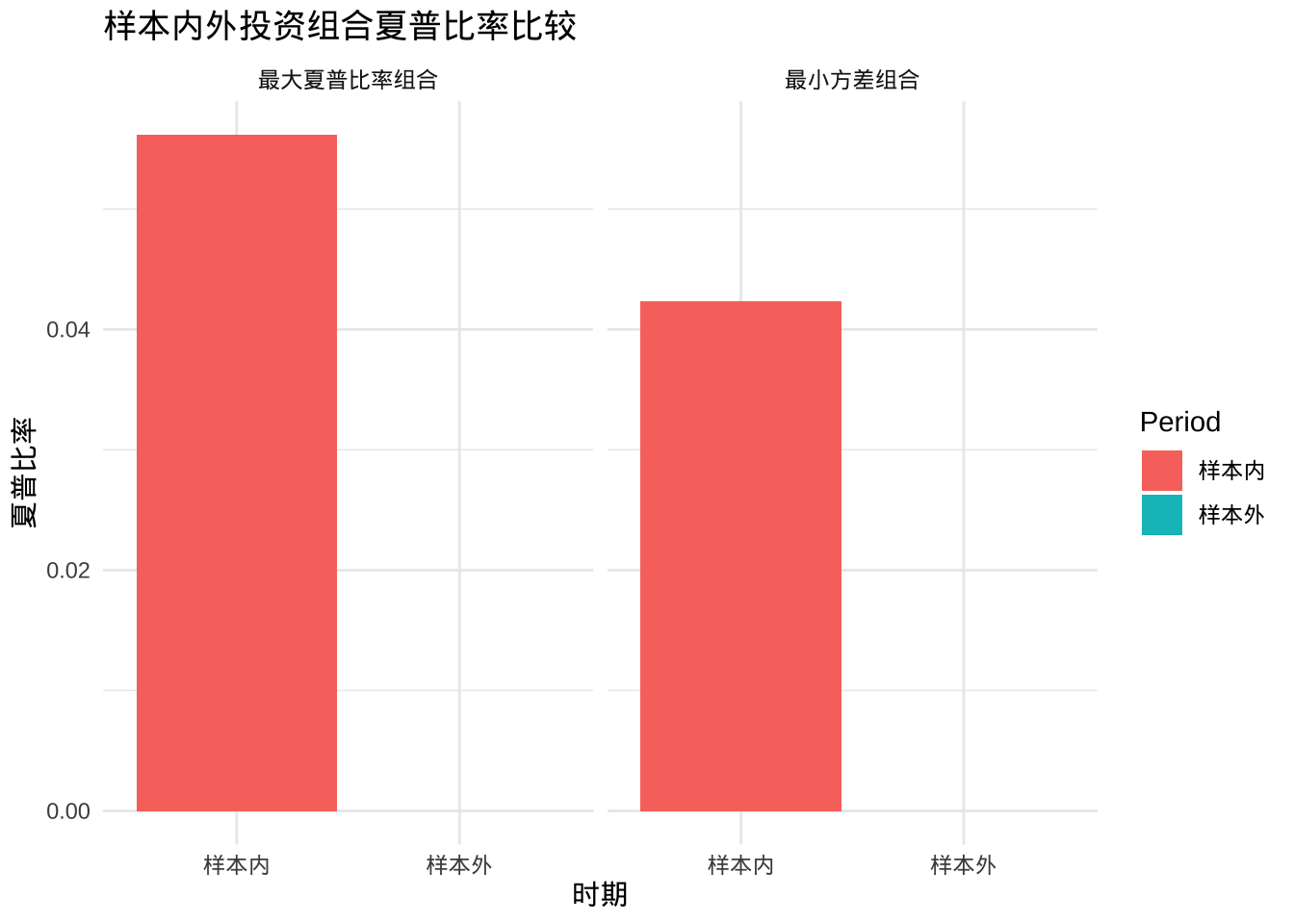
ggplot(comparison, aes(x = Period, y = Sharpe, fill = Period)) +
geom_bar(stat = "identity", position = position_dodge()) +
facet_wrap(~ Portfolio) +
labs(title = "样本内外投资组合夏普比率比较",
x = "时期",
y = "夏普比率") +
theme_minimal()
与等权重投资组合比较
将马克维兹最优投资组合与简单的等权重投资组合进行比较,验证其有效性:
# 计算等权重投资组合在样本内的表现
equal_weights <- rep(1/length(tickers), length(tickers))
equal_return <- sum(annual_returns * equal_weights)
equal_var <- t(equal_weights) %*% cov(returns_matrix * 252) %*% equal_weights
equal_sd <- sqrt(equal_var)
equal_sharpe <- equal_return / equal_sd
# 计算等权重投资组合在样本外的表现
equal_oos_return <- sum(oos_annual_returns * equal_weights)
equal_oos_var <- t(equal_weights) %*% cov(oos_returns_matrix * 252) %*% equal_weights
equal_oos_sd <- sqrt(equal_oos_var)
equal_oos_sharpe <- equal_oos_return / equal_oos_sd
# 创建数据框展示比较结果
comparison_df <- data.frame(
Portfolio = c("等权重组合", "最小方差组合", "最大夏普比率组合"),
InSample_Return = c(equal_return,
min_var_portfolio$Return,
max_sharpe_portfolio$Return
),
InSample_Volatility = c(equal_sd,
min_var_portfolio$Volatility,
max_sharpe_portfolio$Volatility
),
InSample_Sharpe = c(equal_sharpe,
min_var_portfolio$Sharpe,
max_sharpe_portfolio$Sharpe
),
OutSample_Return = c(equal_oos_return,
min_var_oos_return,
max_sharpe_oos_return
),
OutSample_Volatility = c(equal_oos_sd,
min_var_oos_sd,
max_sharpe_oos_sd
),
OutSample_Sharpe = c(equal_oos_sharpe,
min_var_oos_sharpe,
max_sharpe_oos_sharpe)
)
# 展示比较结果
knitr::kable(comparison_df,
caption = "不同投资组合表现比较",
digits = 4,
booktabs = TRUE)
Table: (#tab:equal_weights_comparison)不同投资组合表现比较
| Portfolio | InSample_Return | InSample_Volatility | InSample_Sharpe | OutSample_Return | OutSample_Volatility | OutSample_Sharpe |
|---|---|---|---|---|---|---|
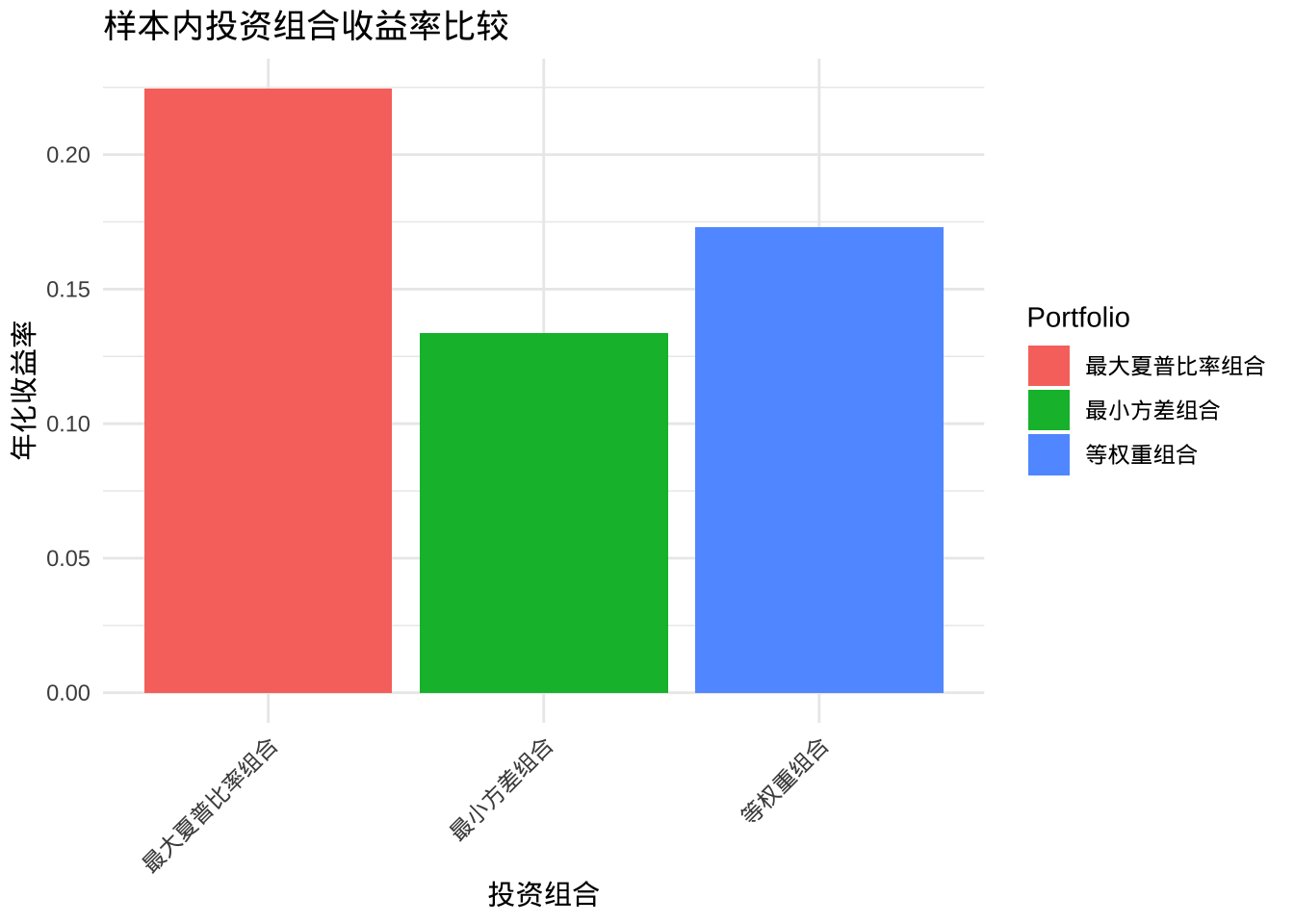
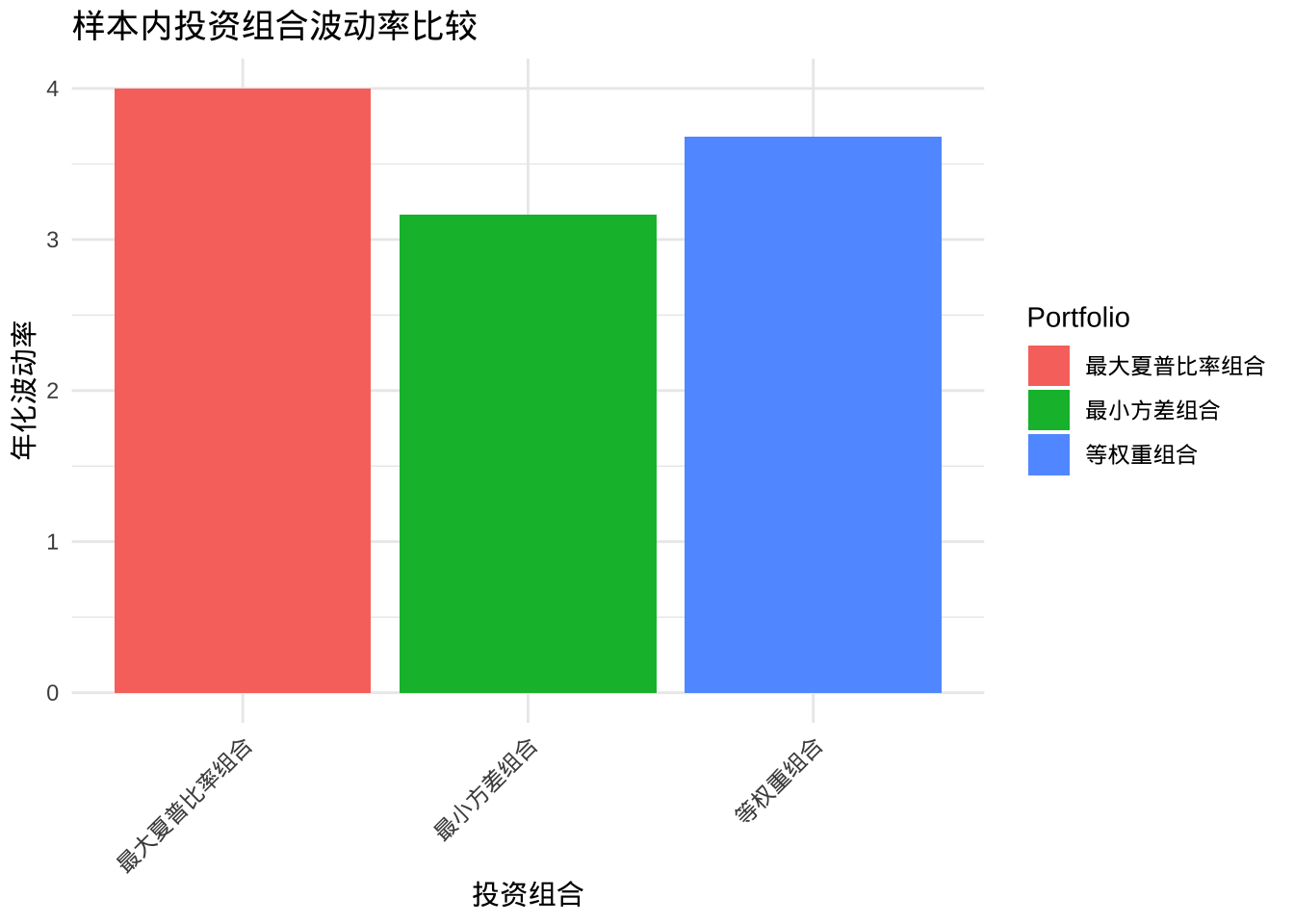
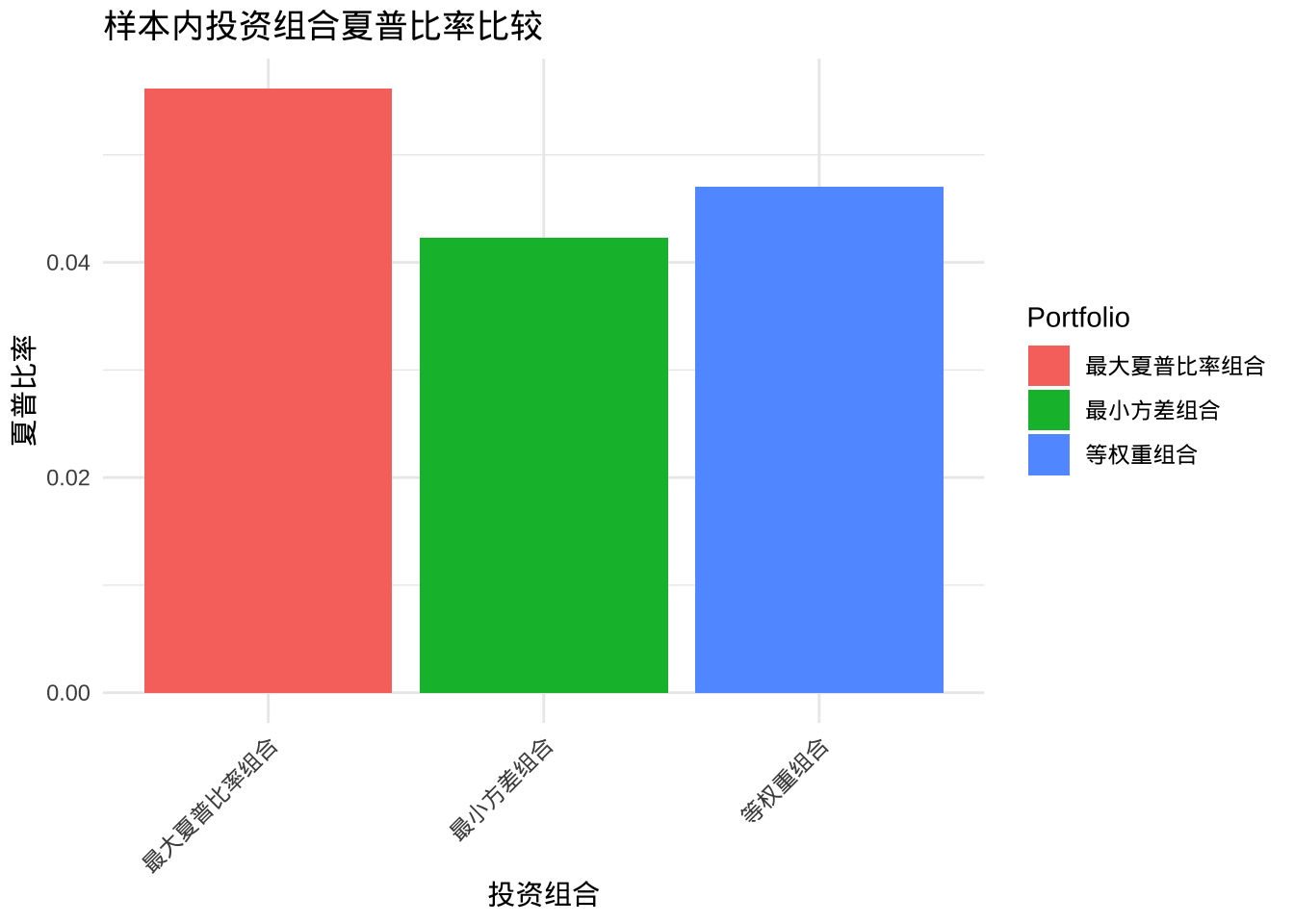
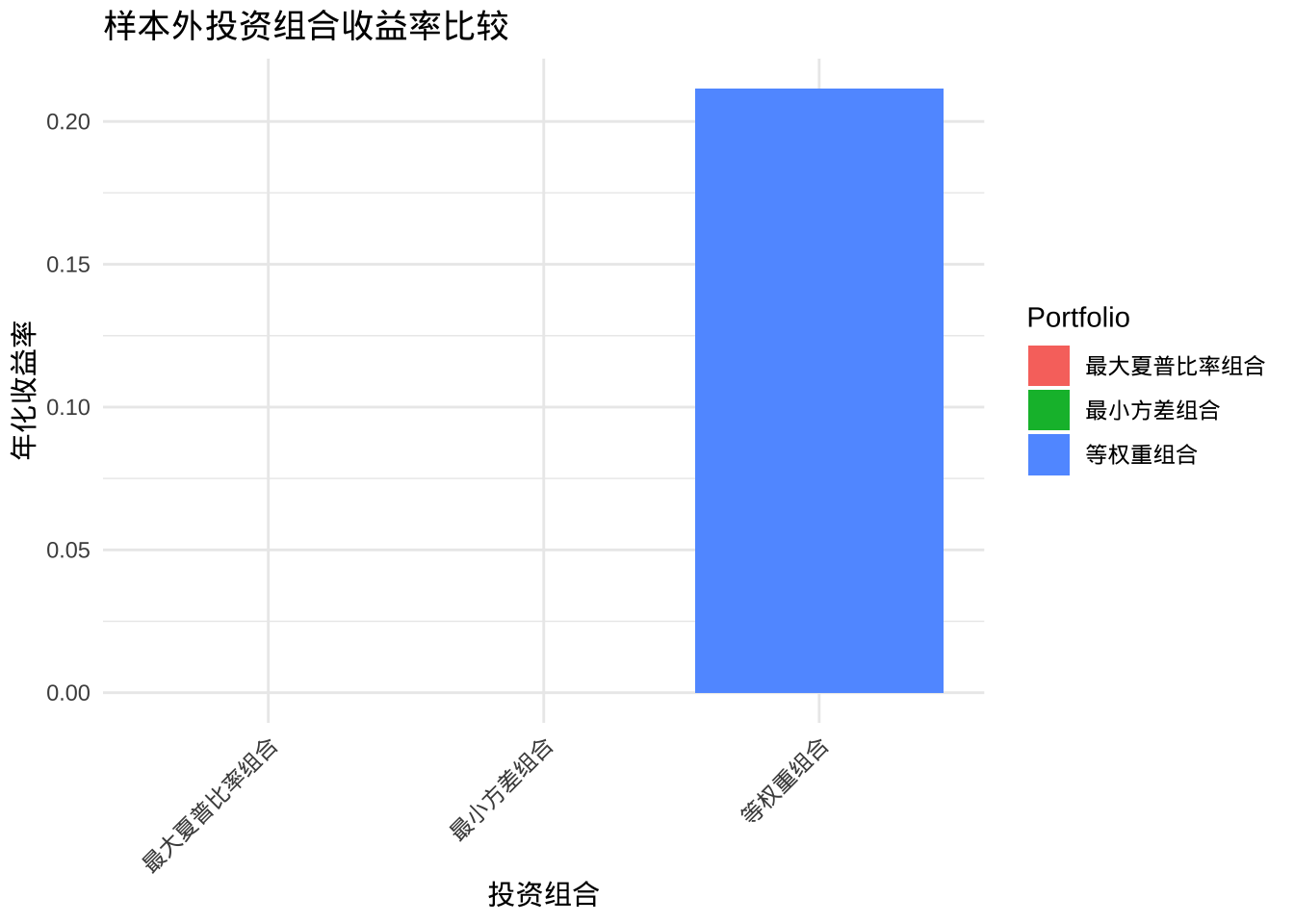
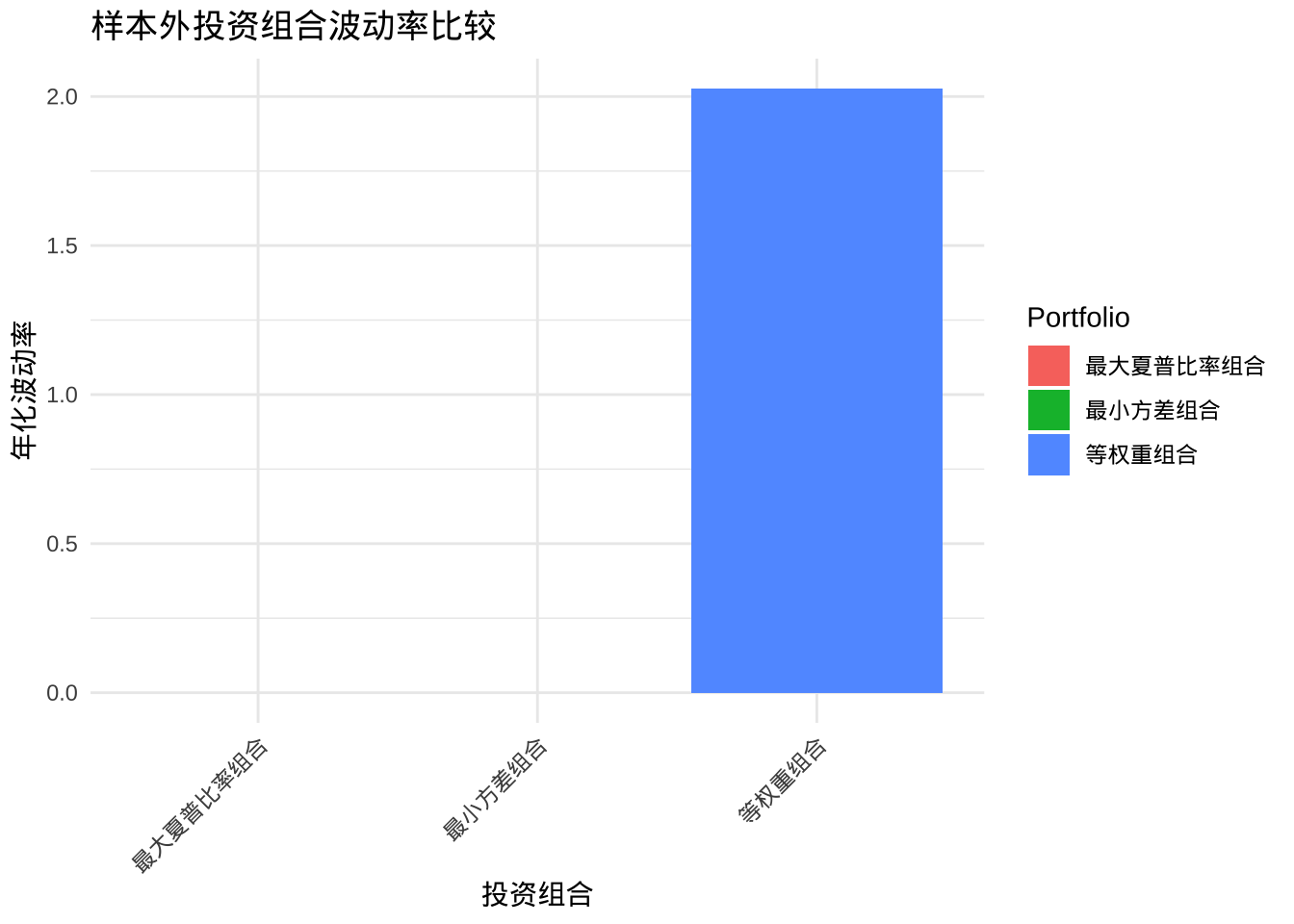
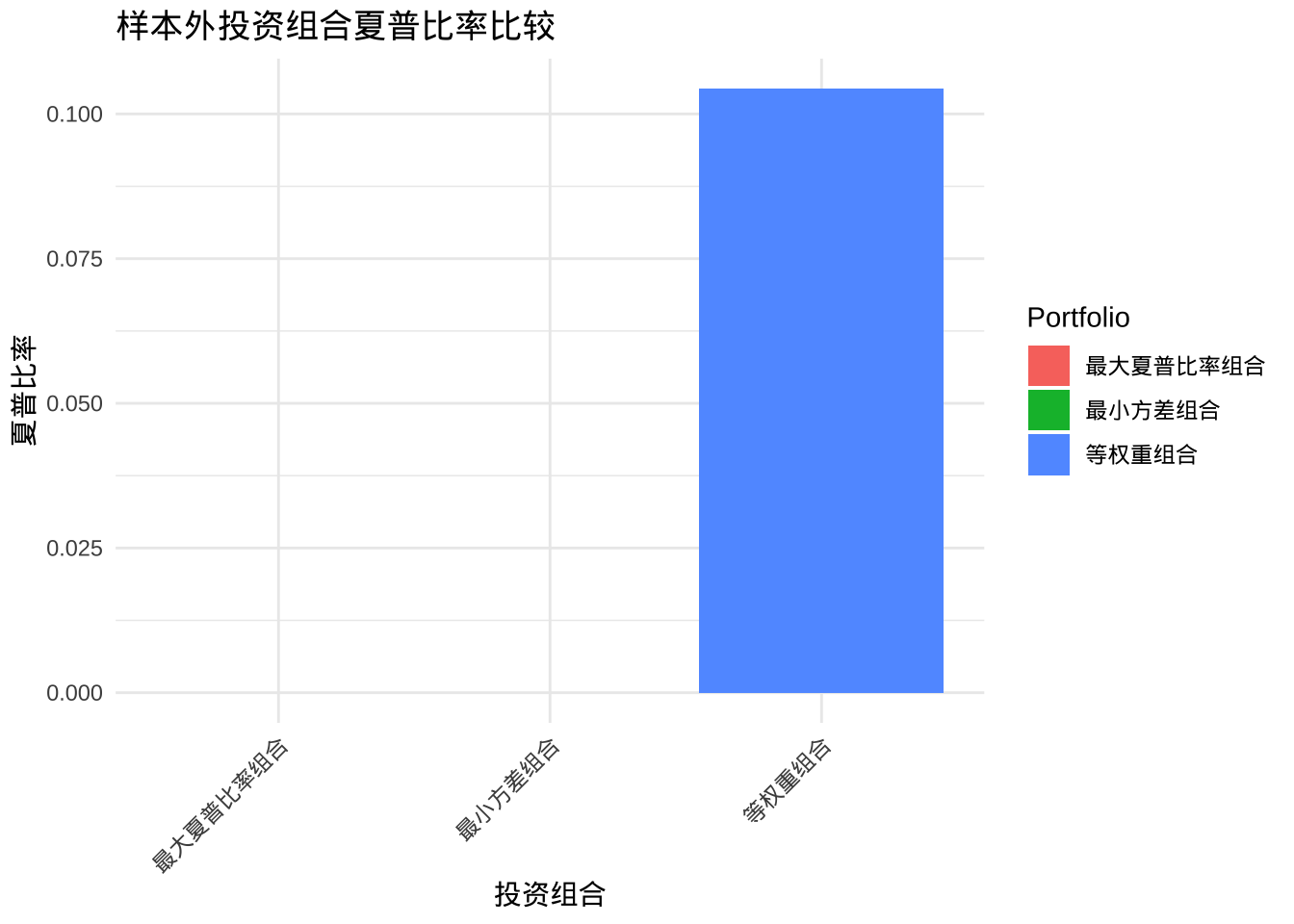
| 等权重组合 | 0.1730 | 3.6809 | 0.0470 | 0.2115 | 2.0263 | 0.1044 |
| 最小方差组合 | 0.1338 | 3.1616 | 0.0423 | NA | NA | NA |
| 最大夏普比率组合 | 0.2245 | 3.9985 | 0.0561 | NA | NA | NA |
# 绘制样本内比较图表
ggplot(comparison_df,
aes(x = Portfolio,
y = InSample_Return,
fill = Portfolio)) +
geom_bar(stat = "identity") +
labs(title = "样本内投资组合收益率比较",
x = "投资组合",
y = "年化收益率") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45,
hjust = 1))
ggplot(comparison_df,
aes(x = Portfolio,
y = InSample_Volatility,
fill = Portfolio)) +
geom_bar(stat = "identity") +
labs(title = "样本内投资组合波动率比较",
x = "投资组合",
y = "年化波动率") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45,
hjust = 1))
ggplot(comparison_df,
aes(x = Portfolio,
y = InSample_Sharpe,
fill = Portfolio)) +
geom_bar(stat = "identity") +
labs(title = "样本内投资组合夏普比率比较",
x = "投资组合",
y = "夏普比率") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45,
hjust = 1))
# 绘制样本外比较图表
ggplot(comparison_df,
aes(x = Portfolio,
y = OutSample_Return,
fill = Portfolio)) +
geom_bar(stat = "identity") +
labs(title = "样本外投资组合收益率比较",
x = "投资组合",
y = "年化收益率") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45,
hjust = 1))
ggplot(comparison_df, aes(x = Portfolio,
y = OutSample_Volatility,
fill = Portfolio)) +
geom_bar(stat = "identity") +
labs(title = "样本外投资组合波动率比较",
x = "投资组合",
y = "年化波动率") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45,
hjust = 1))
ggplot(comparison_df, aes(x = Portfolio,
y = OutSample_Sharpe,
fill = Portfolio)) +
geom_bar(stat = "identity") +
labs(title = "样本外投资组合夏普比率比较",
x = "投资组合",
y = "夏普比率") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45,
hjust = 1))
结论与讨论
研究结论
通过对马克维兹投资组合理论的实证分析,我们得出以下主要结论:
有效前沿的构建:基于历史数据,我们成功构建了包含多只股票的有效前沿,直观展示了风险与收益的权衡关系。
最优投资组合表现:最小方差组合和最大夏普比率组合在样本内均表现出优于单个资产的风险调整后收益。
样本外验证:尽管样本外表现不如样本内,但马克维兹投资组合仍然显示出优于单资产和等权重组合的风险调整后收益,验证了理论在实际应用中的有效性。
多元化投资的价值:通过资产间的相关性分析,我们发现即使是简单的多元化投资(如等权重组合)也能显著降低风险,而优化后的马克维兹投资组合则进一步提升了风险调整后收益。
5.2 局限性与改进方向
本研究存在以下几点局限性:
历史数据依赖:马克维兹模型基于历史数据计算预期收益和风险,而未来市场表现可能与历史数据有较大差异。
参数敏感性:模型对输入参数(特别是预期收益率)非常敏感,小的参数变化可能导致最优权重的显著变化。
未考虑交易成本和税收:实际投资中,交易成本和税收会显著影响投资组合的实际表现。
正态分布假设:模型假设资产收益率服从正态分布,但实际金融市场中往往存在肥尾现象。
未来研究可以考虑以下改进方向:
引入条件协方差矩阵:使用GARCH等模型捕捉时变的波动率和相关性。
考虑高阶矩:扩展模型以纳入偏度和峰度等高阶矩,更好地捕捉非正态分布特性。
加入交易成本和约束:在优化过程中考虑实际投资限制和交易成本。
使用机器学习方法:利用机器学习技术改进预期收益和风险的预测精度。
参考文献
- Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77-91.
- Fabozzi, F. J., & Markowitz, H. M. (2011). The Theory and Practice of Investment Management: Asset Allocation, Valuation, Portfolio Construction, and Strategies. Wiley.
- R Core Team (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.
- Brian G. Peterson and Peter Carl (2023). PerformanceAnalytics: Econometric Tools for Performance and Risk Analysis. R package version 2.0.4.
- Ross Bennett, Dirk Eddelbuettel, and Stephen R. McElroy (2023). PortfolioAnalytics: Portfolio Analysis, Including Numerical Methods for Optimization of Portfolios. R package version 1.5.5.
- Jeffrey A. Ryan and Joshua M. Ulrich (2023). quantmod: Quantitative Financial Modelling Framework. R package version 0.4.24.
- Wickham H. (2016). ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York.
- Wickham H. (2023). dplyr: A Grammar of Data Manipulation. R package version 1.1.3.
- Wickham H., Averick M., Bryan J., Chang W., McGowan L.D., François R., Grolemund G., Hayes A., Henry L., Hester J., Kuhn M., Pedersen T.L., Miller E., Bache S.M., Müller K., Ooms J., Robinson D., Seidel D.P., Spinu V., Takahashi K., Vaughan D., Wilke C., Woo K., Yutani H. (2019). Welcome to the tidyverse. Journal of Open Source Software, 4(43), 1686, https://doi.org/10.21105/joss.01686.